题目内容
2. 如图,将一条两边沿互相平行的纸带折叠,若∠1=30°,则∠α=75°.
如图,将一条两边沿互相平行的纸带折叠,若∠1=30°,则∠α=75°.
分析 由平行线的性质可知∠ABC=∠1,由折叠的性质可知∠CBD+∠ABD=180°,列方程求解.
解答 解:如图,由平行线的性质,得∠ABC=∠1=30°,
由折叠的性质,得∠CBD+∠ABD=180°,
即α+α+∠ABC=180°,
2α+30°=180°,
解得α=75°.
故答案为:75°.
点评 本题考查了折叠的性质,平行线的性质.关键是明确∠CBD与∠ABD的互补关系.

练习册系列答案
相关题目
12.$\sqrt{9}$的值是( )
| A. | ±3 | B. | -3 | C. | 3 | D. | 81 |
13. 如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )
如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )
 如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )
如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )| A. | ∠3+∠4=180° | B. | ∠1+∠8=180° | C. | ∠5+∠7=180° | D. | ∠2+∠6=180° |
17. 如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )
如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )
 如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )
如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )| A. | 8.5 | B. | 9.5 | C. | 9 | D. | 10 |
14.下列定理中,逆命题不成立的是( )
| A. | 两直线平行,内错角相等 | B. | 直角三角形两锐角互余 | ||
| C. | 对顶角相等 | D. | 同位角相等,两直线平行 |
12.已知点N在x轴上,则点M(m,m2-2m+3)与点N的距离最小值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{5}$ |
 按照事件发生概率的大小,将表示该事件的序号标在数轴适当位置:
按照事件发生概率的大小,将表示该事件的序号标在数轴适当位置: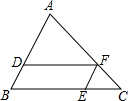 如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.
如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.