题目内容
5.函数y=mx+n与y=nx的大致图象是( )| A. | 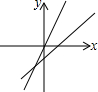 | B. | 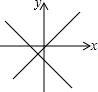 | C. | 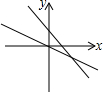 | D. | 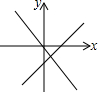 |
分析 由于两条直线y=mx+n与y=nx中都有待定系数n,只需考虑n的正负就可解决问题.
解答 解:当n>0时,直线y=mx+n与y轴交于正半轴,直线y=nx呈上升趋势,排除A和B,
当n<0时,直线y=mx+n与y轴交于负半轴,直线y=nx呈下降趋势,排除C,
故选D.
点评 本题主要考查了一次函数的图象与待定系数的关系,当一次项的系数为正时,图象呈上升趋势,一次项的系数为负时,图象呈下降趋势;当常数项为正时,图象与y轴交于正半轴,当常数项为0时,图象与y轴交于原点,当常数项为负时,图象与y轴交于负半轴.

练习册系列答案
相关题目
20.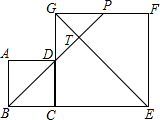 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
10.下列说法错误的是( )
| A. | 6是-6的相反数 | B. | -6是-(-6)的相反数 | ||
| C. | -(+8)与+(-8)互为相反数 | D. | +(-8)与-(-8)互为相反数 |
17.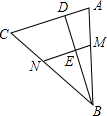 如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )
如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )
 如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )
如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )| A. | BD是△ABC的高 | B. | CD是△BCD的高 | C. | ME是△ABD的高 | D. | BE是△BMN的高 |
15. 如图,下列表述不正确的是( )
如图,下列表述不正确的是( )
 如图,下列表述不正确的是( )
如图,下列表述不正确的是( )| A. | ∠1可表示为∠BAC | B. | ∠2可表示为∠DAC | ||
| C. | ∠DAB可表示为∠BAD | D. | ∠A可表示为∠DAB |
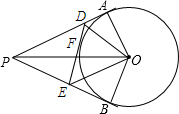 如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.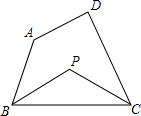 如图,在四边形ABCD中,∠A+∠D=220°,∠ABC的平分线与∠BCD的平分线交于点P,则∠P的度数为110°.
如图,在四边形ABCD中,∠A+∠D=220°,∠ABC的平分线与∠BCD的平分线交于点P,则∠P的度数为110°.