题目内容
15.解下列一元二次方程:(1)x2+6x-2=0(用配方法);
(2)x2+2$\sqrt{2}$x-$\frac{1}{4}$=0(运用求根公式法).
分析 (1)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)求出b2-4ac的值,再代入公式求出即可.
解答 解:(1)x2+6x-2=0,
x2+6x=2,
x2+6x+9=9+2,
(x+3)2=11,
x+3=$±\sqrt{11}$,
x1=-3+$\sqrt{11}$,x2=-3-$\sqrt{11}$;
(2)x2+2$\sqrt{2}$x-$\frac{1}{4}$=0,
b2-4ac=(2$\sqrt{2}$)2-4×1×(-$\frac{1}{4}$)=9,
x=$\frac{-2\sqrt{2}±\sqrt{9}}{2}$,
x1=$\frac{-2\sqrt{2}+3}{2}$,x2=$\frac{-2\sqrt{2}-3}{2}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
6.将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
| A. | 2、3、4 | B. | 4、5、6 | C. | 5、11、12 | D. | 8、15、17 |
4.下列等式一定成立的是( )
| A. | a2+a3=2a5 | B. | a2•a3=a5 | C. | (2ab2)3=6a3b6 | D. | a6÷a3=a2 |
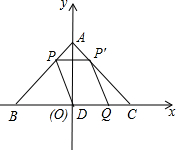 在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.
在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.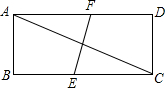 矩形ABCD中,AD=5,AB<4,将矩形ABCD折起来,使A、C两顶点重合,若折痕EF=$\sqrt{6}$,求AB的长.
矩形ABCD中,AD=5,AB<4,将矩形ABCD折起来,使A、C两顶点重合,若折痕EF=$\sqrt{6}$,求AB的长.