题目内容
在梯形ABCD中,AB∥CD,AC、BD相交于点E,且
=3,S△ADE=6cm2,求梯形ABCD的面积.
| CE |
| AE |
考点:梯形
专题:
分析:根据S△ADE与S△CDE是等高不等底,且CE:AE=3:1,得出S△CDE=3S△ADE=18cm2,由S△ABD与S△ABC是等底等高,得出S△ABC=S△ABD,进而求得S△BEC=S△ADE=6cm2,由S△ABE与S△BCE是等高不等底,且CE:AE=3:1,得出S△ABE=
S△BCE=2cm2.即可求得梯形ABCD的面积=S△ADE+S△CDE+S△BCE+S△ABE=32cm2.
| 1 |
| 3 |
解答: 解:∵S△ADE与S△CDE是等高不等底,且CE:AE=3:1,
解:∵S△ADE与S△CDE是等高不等底,且CE:AE=3:1,
∴S△CDE=3S△ADE=18cm2
∵S△ABD与S△ABC是等底等高,
∴S△ABC=S△ABD,
∴S△BEC=S△ADE=6cm2,(两边同时减去S△ABE)
又∵S△ABE与S△BCE是等高不等底,且CE:AE=3:1,
∴S△ABE=
S△BCE=2cm2.
∴梯形ABCD的面积=S△ADE+S△CDE+S△BCE+S△ABE=6+18+6+2=32(cm2)
 解:∵S△ADE与S△CDE是等高不等底,且CE:AE=3:1,
解:∵S△ADE与S△CDE是等高不等底,且CE:AE=3:1,∴S△CDE=3S△ADE=18cm2
∵S△ABD与S△ABC是等底等高,
∴S△ABC=S△ABD,
∴S△BEC=S△ADE=6cm2,(两边同时减去S△ABE)
又∵S△ABE与S△BCE是等高不等底,且CE:AE=3:1,
∴S△ABE=
| 1 |
| 3 |
∴梯形ABCD的面积=S△ADE+S△CDE+S△BCE+S△ABE=6+18+6+2=32(cm2)
点评:本题考查了梯形的性质,三角形的面积,解答此题的主要依据是:等高不等底的三角形的面积比就等于其对应底的比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③x2+2x-3;④3x2-
=0.
①3x2+7=0;②ax2+bx+c=0;③x2+2x-3;④3x2-
| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
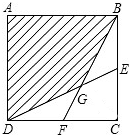 如图,已知正方形ABCD的边长为3,E、F分别是BC、DC的中点,BF、DE相交于点G,求四边形ABGD的面积.
如图,已知正方形ABCD的边长为3,E、F分别是BC、DC的中点,BF、DE相交于点G,求四边形ABGD的面积.