题目内容
11.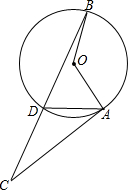 如图,点A,D,B为⊙O上的三点,∠AOB=120°,且过A的直线交BD延长线于点C,连接AD,且AD=CD,则∠C的度数为30°.
如图,点A,D,B为⊙O上的三点,∠AOB=120°,且过A的直线交BD延长线于点C,连接AD,且AD=CD,则∠C的度数为30°.
分析 由等腰三角形的性质得出∠C=∠DAC,由圆周角定理求出∠ADB=$\frac{1}{2}$∠AOB=60°,再由三角形的外角性质即可得出结果.
解答 解:∵AD=CD,
∴∠C=∠DAC,
∵∠ADB=$\frac{1}{2}$∠AOB=60°,
∴∠C=∠DAC=$\frac{1}{2}$∠ADB=30°;
故答案为:30°.
点评 本题考查了圆周角定理、等腰三角形的性质、三角形的外角性质.此题难度适中,熟练掌握圆周角定理和等腰三角形的性质是解决问题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
1.某市需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成.求实际每天铺设管道的长度与实际施工天数.小宇同学根据题意列出方程:$\frac{660}{x}-\frac{660}{x(1+10%)}=6$.则方程中未知数x所表示的量是( )
| A. | 实际每天铺设管道的长度 | B. | 实际施工的天数 | ||
| C. | 原计划每天铺设管道的长度 | D. | 原计划施工的天数 |
19.下列四组数分别是三条线段的长度,能构成三角形的是( )
| A. | 1,1,2 | B. | 1,3,4 | C. | 2,3,6 | D. | 4,5,8 |
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}>0$;③ac-b+1=0;④OA•OB=-$\frac{c}{a}$.其中正确结论的序号是①③④.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}>0$;③ac-b+1=0;④OA•OB=-$\frac{c}{a}$.其中正确结论的序号是①③④.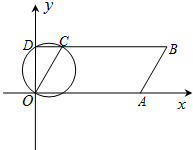 如图,在平面直角坐标系中,以OC为直径的圆交y轴于点D,∠DOC=30°,OC=2.延长DC至点B,使得CB=4DC,过B点作BA∥OC交x轴于A点.
如图,在平面直角坐标系中,以OC为直径的圆交y轴于点D,∠DOC=30°,OC=2.延长DC至点B,使得CB=4DC,过B点作BA∥OC交x轴于A点. 如图,点A、B、C、D在同一直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.
如图,点A、B、C、D在同一直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC. 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,其中一定成立的是①②④(把所有正确结论的序号都填在横线上)
如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,其中一定成立的是①②④(把所有正确结论的序号都填在横线上)