题目内容
20. 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,其中一定成立的是①②④(把所有正确结论的序号都填在横线上)
如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,其中一定成立的是①②④(把所有正确结论的序号都填在横线上)
分析 根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定△ADG≌△FDG,再由GF+GB=GA+GB=12,EB=EF,△BGE为直角三角形,可通过勾股定理列方程求出AG=4,BG=8,进而求出△BEF的面积,再抓住△BEF是等腰三角形,而△GED显然不是等腰三角形,判断③是错误的.
解答 解:由折叠可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
∴△ADG≌△FDG,①正确;
∵正方形边长是12,
∴BE=EC=EF=6,
设AG=FG=x,则EG=x+6,BG=12-x,
由勾股定理得:EG2=BE2+BG2,
即:(x+6)2=62+(12-x)2,
解得:x=4
∴AG=GF=4,BG=8,BG=2AG,②正确;
BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,③错误;
S△GBE=$\frac{1}{2}$×6×8=24,S△BEF=$\frac{EF}{EG}$•S△GBE=$\frac{6}{10}$×24=$\frac{72}{5}$,④正确;
故答案为:①,②,④.
点评 本题综合性较强,考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算,有一定的难度.

练习册系列答案
相关题目
10.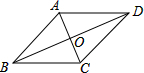 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | OA=OC |
8.未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为( )亿元.
| A. | 0.845×104 | B. | 8.45×103 | C. | 8.45×104 | D. | 84.5×102 |
15.∠α=35°,则∠α的余角的度数为( )
| A. | 65° | B. | 55° | C. | 45° | D. | 25° |
12.下列汽车标志图案中既是轴对称图形也是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.某种病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( )
| A. | 1.2×10-7米 | B. | 1.2×10-8米 | C. | 1.2×10-9米 | D. | 12×10-8米 |
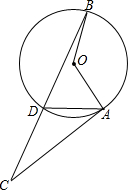 如图,点A,D,B为⊙O上的三点,∠AOB=120°,且过A的直线交BD延长线于点C,连接AD,且AD=CD,则∠C的度数为30°.
如图,点A,D,B为⊙O上的三点,∠AOB=120°,且过A的直线交BD延长线于点C,连接AD,且AD=CD,则∠C的度数为30°.