题目内容
19. 在△ABC中,∠B=22.5°,∠C=30°,AB的垂直平分线OD交BC边于点D,连结AD
在△ABC中,∠B=22.5°,∠C=30°,AB的垂直平分线OD交BC边于点D,连结AD(1)求∠DAC的度数;
(2)若AC=4cm,求△ABC的面积(结果保留根号)
分析 (1)根据线段的垂直平分线的性质得到AD=BD,得到∠B=∠BAD=22.5°,根据三角形外角的性质求出∠ADC=45°,根据三角形内角和定理计算即可;
(2)过A点作AE⊥BC于点E,则AE=DE,根据直角三角形的性质求出AE、BC的长,根据三角形面积公式计算即可.
解答 解:(1)∵OD是AB的垂直平分线;
∴AD=BD,
∴∠B=∠BAD=22.50,
∴∠ADC=45°,
∵∠A=30°,
∴∠DAC=105°;
(2)过A点作AE⊥BC于点E,则AE=DE, 在Rt△ACE中,
在Rt△ACE中,
∵AC=4,
∴AE=2,EC=2$\sqrt{3}$,
∴DE=2,
在Rt△AED中,
AD=2$\sqrt{2}$,
∴AD=BD=2$\sqrt{2}$,
∴BC=2$\sqrt{2}$+2$\sqrt{3}$+2
∴S△ABC=$\frac{1}{2}AE•BC$=$\frac{1}{2}×2×$($2\sqrt{2}+2\sqrt{3}+2$)=($2\sqrt{2}+2\sqrt{3}+2$).
点评 本题考查的是线段的垂直平分线的性质、直角三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 已知:∠AOB=60°,∠B0C=30°,OE是∠AOB平分线,求∠COE度数.
已知:∠AOB=60°,∠B0C=30°,OE是∠AOB平分线,求∠COE度数.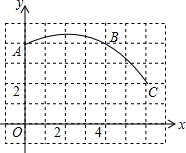 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作: △BDA、△HDC都是等腰直角三角形,且D在BC上,BH的延长线与 AC交于点E,请你在图中找出一对全等三角形,并写出证明过程.
△BDA、△HDC都是等腰直角三角形,且D在BC上,BH的延长线与 AC交于点E,请你在图中找出一对全等三角形,并写出证明过程. 数学活动课上,同学们围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”其中一位同学作出了如图所示的图形.你认为他的作法的理由有到线段两端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.
数学活动课上,同学们围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”其中一位同学作出了如图所示的图形.你认为他的作法的理由有到线段两端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.