题目内容
16．已知关于x的方程x2-ax+2a-4=0（1）求证：不论a取何实数，该方程都有实数根；
（2）若该方程的两个根为连续的偶数，求a的值及对应的方程的根．
分析 （1）根据方程的系数结合根的判别式即可得出△=（a-4）2≥0，此题得证；
（2）利用因式分解法解一元二次方程即可得出方程的两个根，结合该方程的两个根为连续的偶数即可得出关于a的一元一次方程，解之即可得出结论．
解答 （1）证明：在方程x2-ax+2a-4=0中，△=a2-4（2a-4）=a2-8a+16=（a-4）2，
∵（a-4）2≥0，
∴不论a取何实数，该方程都有实数根；
（2）解：∵x2-ax+2a-4=（x-2）（x-a+2）=0，
解得：x1=2，x2=a-2，
∵两个根为连续的偶数，
∴x2=a-2=0或4，
∴a=2或6．
点评 本题考查了根的判别式以及因式分解法解一元二次方程，利用因式分解法解出方程的两个根为x1=2、x2=a-2是解题的关键．
练习册系列答案
相关题目
如图所示，船A和船B同时从小岛O出发，船A沿北偏西20°的方向航行，船B沿北偏东70°的方向航行．
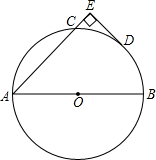如图，AB为⊙O直径，D为BC弧的中点，DE⊥AC于E，
已知四边形ABCD是⊙O的内接四边形，∠ABC=2∠D，连接OC、OA、AC．