题目内容
17.已知△ABC的周长为84cm,b+6a=6c,a:c=7:8,问能否以a、b、c为三边组成△ABC?如果能,试求出这三边;如果不能,请说明理由.分析 可设a=7x,则c=8x,代入b+6a=6c,得到b=6x,则根据等量关系:△ABC的周长为84cm,列出方程求得x的值,进一步即可求解.
解答 解:设a=7xcm,则c=8xcm,代入b+6a=6c,得到b=6xcm,依题意有
7x+6x+8x=84,
解得x=4,
则7x=28,6x=24,8x=32,
∵24+28>32,
∴三边长分别为28cm,24cm,32cm.
点评 考查了三角形三边关系,在涉及三角形的边长或周长的计算时,注意最后要用三边关系去检验,这是一个隐藏的定时炸弹,容易忽略.

练习册系列答案
相关题目
5. 如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )
如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )
 如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )
如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )| A. | 42° | B. | 48° | C. | 52° | D. | 58° |
12.若(x+3y)2=(x-3y)2+M,则M为( )
| A. | 6xy | B. | 12xy | C. | -6xy | D. | -12xy |
6. 下面几何体的左视图是( )
下面几何体的左视图是( )
 下面几何体的左视图是( )
下面几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
7.在平行四边形ABCD中,AD=3,AB=2,则它的周长是( )
| A. | 10 | B. | 6 | C. | 5 | D. | 4 |
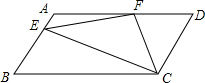 如图所示,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段上,连接EF、CF,则下列结论
如图所示,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段上,连接EF、CF,则下列结论