Question

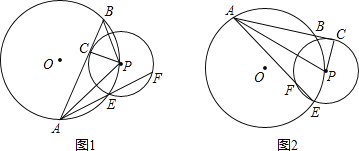
【题目】如图，P是⊙O上的一个点，⊙P与⊙O的一个交点是E，⊙O的弦AB（或延长线）与⊙P相切，C是切点，AE（或延长线）交⊙P于点F，连接PA、PB，设⊙O的半径为R，⊙P的半径为r（R＞r），

（1）如图1，求证：PAPB＝2rR；

（2）如图2，当切点C在⊙O的外部时，（1）中的结论是否成立，试证明之；

（3）探究（图2）已知PA＝10，PB＝4，R＝2r，求EF的长．

Answer 1

【答案】（1）证明见解析；（2）结论还成立；（3）．

【解析】

（1）连接PO并延长交⊙O于H，连接AH、PC，通过进行求解即可得解；

（2）通过进行求解即可得解；

（3）过P作AE的垂线，垂足是Q，连接PE，通过及垂径定理进行求解即可得解.

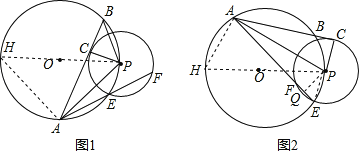
（1）证明：如下图1，连接PO并延长交⊙O于H，连接AH、PC，

∵AB是⊙P的切线

∴，

∵PH是直径，

∴，

∵∠PCB＝∠PAH，

∵∠PBC＝∠PHA，

∴，

∴，

∵，

∴；

（2）结论还成立，

证明：如下图1：由（1）得：，

∴，

∵，

∴；

（3）解：如下图2，过P作AE的垂线，垂足是Q，连接PE，

∵PA＝10，PB＝4，R＝2r，

而，

∴，

在和中，

，

∴，

∴，

∴PQ＝，

∴QE＝，

由垂径定理得：EF＝2QE＝．