题目内容
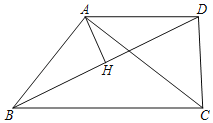
【题目】如图1,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒1个单位长度,点
移动,速度为每秒1个单位长度,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
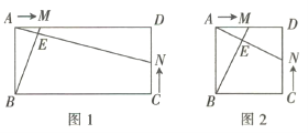
(1)若两点的运动时间为![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
(2)在(1)的情况下,猜想![]() 与
与![]() 的位置关系并证明你的结论.
的位置关系并证明你的结论.
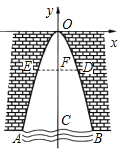
(3)①如图2,当![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________.
_________.
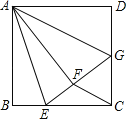
②当![]() ,
,![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________(用含
_________(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)①
,证明见解析;(3)①![]() ;②
;②![]()
【解析】
(1)根据相似三角形的性质,可得![]() ,进而列出方程,求出t的值.
,进而列出方程,求出t的值.
(2)根据相似三角形的性质,可得![]() ,进而根据等量关系以及矩形的性质,得出
,进而根据等量关系以及矩形的性质,得出![]() ,进而得出结论.
,进而得出结论.
(3)①根据全等三角形的判定,可得出△AMB≌△DNA,再根据全等三角形的性质,即可得出AM=DN,得出方程,求解即可得出答案.
解:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
解得![]() .
.
(2)![]() .
.
证明:∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
(3)①∵![]()
∴∠ABE+∠BAE=90°
∵![]()
∴![]()
∵AD=AB,∠BAD=∠ADC=90°
∴△AMB≌△DNA
∴AM=DN
∴t=2-2t
∴t=![]()
②∵由①知![]() ,∠BAD=∠ADC=90°
,∠BAD=∠ADC=90°
∴![]()
∵![]()
∴![]() =n
=n
∴![]()
∴t=![]()

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.