题目内容
【题目】画出抛物线y＝﹣
（x﹣1）2+5的图象（要求列表，描点），回答下列问题：
（1）写出它的开口方向，对称轴和顶点坐标；
（2）当y随x的增大而增大时，写出x的取值范围；
（3）若抛物线与x轴的左交点（x1，0）满足n≤x1≤n+1，（n为整数），试写出n的值．
【答案】列表画图见解析；（1）开口向上，对称轴是直线x＝1，顶点坐标为（1，5）；（2）x＜1；（3）n＝﹣3
【解析】
根据二次函数图象的画法，先列表，然后描点、连线即可画出该抛物线的图象；
（1）根据画出的抛物线的图象，可以写出它的开口方向，对称轴和顶点坐标；
（2）根据函数图象，可以写出当y随x的增大而增大时，x的取值范围；
（3）令y＝0求出相应的x的值，即可得到x1的值，然后根据n≤x1≤n+1，（n为整数），即可得到n的值．
解：列表：
描点、连线
（1）由图象可知，
该抛物线开口向上，对称轴是直线x＝1，顶点坐标为（1，5）；
（2）由图象可知，当y随x的增大而增大时，x的取值范围是x＜1；
（3）当y＝0时，
0＝﹣
（x﹣1）2+5，
解得，
，
，
则该抛物线与x轴的左交点为（
+1，0），
∵﹣3＜+1＜﹣2，n≤x1≤n+1，（n为整数），
∴n＝﹣3．
【题目】中华文明，源远流长：中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
成绩x/分 | 频数 | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 20 | 0.10 |
70≤x＜80 | 30 | b |
80≤x＜90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
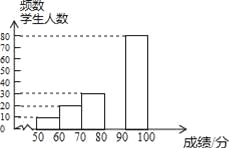
请根据所给信息，解答下列问题：
（1）a=______，b=______；
（2）请补全频数分布直方图；
（3）这次比赛成绩的中位数会落在_____________分数段；
（4）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？
【题目】水是人类的生命之源，为了鼓励居民节约用水，相关部门实行居民生活用水阶梯式计量水价政策，下表是昆明市居民“一表一户”生活用水阶梯式计费价格表的部分信息，请解答：
自来水销售价格 | |
每户每月用水量 | 单位：元/吨 |
15吨及以下 | a |
超过15吨但不超过25吨的部分 | b |
超过25吨的部分 | 5 |
（1）小王家今年3月份用水22吨，要交水费 元（用含a，b的代数式表示）；
（2）小王家今年4月份用水21吨，交水费48元；邻居小李家4月份用水27吨，交水费70元，求a，b的值；
（3）如果小王家5月份用水水费计划不超过67元，则小王家5月份最多可用水多少吨？
