题目内容
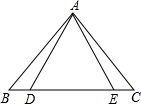如图，△ABE≌△ACD，AB=AC，BE=CD，∠B=60°，∠AEC=120°，则∠DAC的度数等于（ ）| A、120° | B、70° |
| C、60° | D、50° |
考点：全等三角形的性质
专题：
分析：根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE，再根据全等三角形对应角相等可得∠DAC=∠BAE．
解答：解：∵∠B=60°，∠AEC=120°，
∴∠BAE=∠AEC-∠B=120°-60°=60°，
∵△ABE≌△ACD，
∴∠DAC=∠BAE=60°．
故选C．
∴∠BAE=∠AEC-∠B=120°-60°=60°，
∵△ABE≌△ACD，
∴∠DAC=∠BAE=60°．
故选C．
点评：本题考查了全等三角形对应角相等的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并准确识图是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
第九届中国国际园林博览会正在北京丰台举行，预计参观人数17000000人次，是国内园林花卉界最高层次的盛会，将17000000用科学记数法表示应为（ ）
| A、0.17×108 |
| B、17×106 |
| C、1.7×107 |
| D、1.7×108 |
如图，将△ABC绕点A旋转后得到△ADE，则旋转方式为（ ）| A、顺时针旋转90° |
| B、逆时针旋转90° |
| C、顺时针旋转45° |
| D、逆时针旋转45° |
如图，△OAB绕点O逆时针旋转85°到△OCD的位置，已知∠A=80°，∠D=60°则∠AOD等于（ ）| A、55° | B、45° |
| C、40° | D、35° |
若分式
的值为0，则a的值等于（ ）
| a2-4 |
| (a+2)(a-3) |
| A、2和-2 | B、2 | C、-2 | D、3 |
在分式
，
，
，
中，最简分式有（ ）
| b |
| 8a |
| a-b |
| a+b |
| x-y |
| x2+y2 |
| x-y |
| x2-y2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
把分式
中的x和y都扩大为原来的2倍，则分式的值（ ）
| xy |
| x-3y |
| A、不变 | ||
| B、扩大为原来的2倍 | ||
C、缩小为原来的
| ||
| D、扩大为原来的4倍 |