题目内容
14.先化简再求值:$\frac{a}{{a}^{2}-4}÷\frac{{a}^{2}-3a}{a+2}-\frac{1}{2-a}$,其中a满足与2和3构成△ABC的三边,且a为整数.分析 先根据分式混合运算的法则把原式进行化简,再根据三角形的三边关系判断出a的取值范围,选取合适的a的值代入进行计算即可.
解答 解:原式=$\frac{a}{(a-2)(a-3)}$•$\frac{a+2}{a(a-3)}$+$\frac{1}{a-2}$
=$\frac{1}{(a-2)(a-3)}$+$\frac{a-3}{(a-2)(a-3)}$
=$\frac{a-2}{(a-2)(a-3)}$
=$\frac{1}{a-3}$,
∵a与2、3构成△ABC的三边,
∴3-2<a<3+2,即1<a<5,
∵a为整数,
∴a=2、3、4,
当a=2时,分母2-a=0,舍去;当a=3时,分母a-3=0,舍去;故a的值只能为4.
∴当a=4时,原式=$\frac{1}{4-3}$=1.
点评 本题考查的是分式的化简求值,在选取a的值时要保证分式有意义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列运算正确的是( )
| A. | -2(a-1)=-2a+1 | B. | (x3y)2=x5y2 | C. | x8÷x2=x6 | D. | (x+3)2=x2+9 |
6. 如图是由5个相同的正方体组成的立体图形,它的主视图是( )
如图是由5个相同的正方体组成的立体图形,它的主视图是( )
 如图是由5个相同的正方体组成的立体图形,它的主视图是( )
如图是由5个相同的正方体组成的立体图形,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
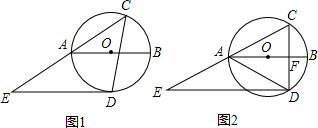
 如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E,若DE=1,∠C=30°,则图中阴影部分的面积是$\frac{4}{9}$π-$\frac{\sqrt{3}}{3}$.
如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E,若DE=1,∠C=30°,则图中阴影部分的面积是$\frac{4}{9}$π-$\frac{\sqrt{3}}{3}$.