题目内容
14.我们可以把|x-y|理解为数轴上表示x的点到表示y的点距离.若2≤x≤4,则|x+1|+|x-2|+|x-3|的最小值和最大值分别为( )| A. | 4,8 | B. | 4,9 | C. | 5,8 | D. | 5,9 |
分析 分两种情况讨论:①当2≤x≤3时,②当3≤x≤4时,先化简|x+1|+|x-2|+|x-3|,再根据x的取值范围得到最小值和最大值,从而求解.
解答 解:①当2≤x≤3时,
|x+1|+|x-2|+|x-3|
=x+1+x-2+3-x
=x+2,
当x=2时,最小值为4,
当x=3时,最大值为5;
②当3≤x≤4时,
|x+1|+|x-2|+|x-3|
=x+1+x-2+x-3
=3x-4
当x=3时,最小值为5,
当x=4时,最大值为8.
综上所述,|x+1|+|x-2|+|x-3|的最小值和最大值分别为4,8.
故选:A.
点评 考查了绝对值和分类思想的运用,如果用字母a表示有理数,则数a绝对值要由字母a本身的取值来确定:①当a是正有理数时,a的绝对值是它本身a; ②当a是负有理数时,a的绝对值是它的相反数-a; ③当a是零时,a的绝对值是零.

练习册系列答案
相关题目
19.下列各点中在函数y=2x-1的图象上的点是( )
| A. | (-1,2) | B. | (1,3) | C. | (2,3) | D. | (2,1) |
6.已知菱形的边长和一条对角线的长均为2,菱形的面积为( )
| A. | 4 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
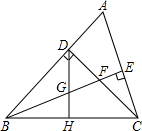 已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.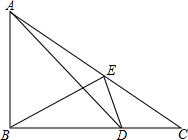 如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.
如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.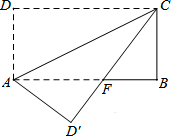 如图,已知长方形ABCD纸片,AB=8,BC=4,若将纸片沿AC折叠,点D落在D′,则重叠部分的面积为10.
如图,已知长方形ABCD纸片,AB=8,BC=4,若将纸片沿AC折叠,点D落在D′,则重叠部分的面积为10.