题目内容
4.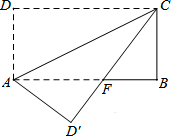 如图,已知长方形ABCD纸片,AB=8,BC=4,若将纸片沿AC折叠,点D落在D′,则重叠部分的面积为10.
如图,已知长方形ABCD纸片,AB=8,BC=4,若将纸片沿AC折叠,点D落在D′,则重叠部分的面积为10.
分析 过点F作FE⊥AC,垂足为E,由勾股定理得:AC=4$\sqrt{5}$,然后证明△ACF为等腰三角形,由等腰三角形的性质可求得AE的长,接下来证明△AEF∽△ABC,从而可求得EF的长为$\sqrt{5}$,最后根据三角形的面积公式求得△ACF的面积即可.
解答 解:如图所示:过点F作FE⊥AC,垂足为E.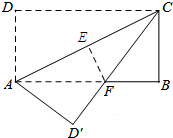
由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{5}$.
∵DC∥AB,
∴∠DCA=∠CAB.
由翻折的性质可知:∠DCA=∠D′CA.
∴∠FAC=∠FCA.
∴AF=CF.
又∵FE⊥AC.
∴AE=CE=2$\sqrt{5}$.
∵∠EAF=∠BAC,∠FEA=∠CBA=90°,
∴△AEF∽△ABC.
∴$\frac{AE}{AB}=\frac{EF}{CB}$,即$\frac{2\sqrt{5}}{8}=\frac{EF}{4}$.
∴EF=$\sqrt{5}$.
∴${S}_{△ACF}=\frac{1}{2}AC•EF=\frac{1}{2}×4\sqrt{5}×\sqrt{5}$=10.
故答案为:10.
点评 本题主要考查的是相似三角形的性质和判定、勾股定理、翻折变换,证得△ACF为等腰三角形,由等腰三角形的性质可求得AE的长是解题的关键.

练习册系列答案
相关题目
14.我们可以把|x-y|理解为数轴上表示x的点到表示y的点距离.若2≤x≤4,则|x+1|+|x-2|+|x-3|的最小值和最大值分别为( )
| A. | 4,8 | B. | 4,9 | C. | 5,8 | D. | 5,9 |
15.下列各线中,不属于等腰三角形“三线合一”的线是( )
| A. | 顶角的平分线 | B. | 底边上的中线 | C. | 底边上的中垂线 | D. | 底边上的高线 |
19.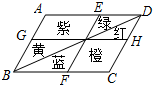 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )| A. | 球落在红花丛中和绿花丛中的概率相等 | |
| B. | 球落在紫花丛中和橙花丛中的概率相等 | |
| C. | 球落在红花丛中和蓝花丛中的概率相等 | |
| D. | 球落在蓝花丛中和黄花丛中的概率相等 |
9.函数y=kx与y=-$\frac{k}{x}$在同一坐标系内的大致图象是( )
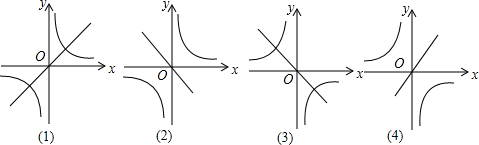

| A. | (1)和(2) | B. | (1)和(3) | C. | (2)和(3) | D. | (2)和(4) |
14.下列运算中,正确的是( )
| A. | (-a2b3)2=a4b6 | B. | (-2a)2=-4a2 | C. | (a+b)2=a2+b2 | D. | b2•b3=2b3 |