题目内容
6. 如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是优弧$\widehat{EF}$上的一点,且∠EPF=50°,则图中阴影部分的面积是6-$\frac{10}{9}$π.
如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是优弧$\widehat{EF}$上的一点,且∠EPF=50°,则图中阴影部分的面积是6-$\frac{10}{9}$π.
分析 由于BC切⊙A于D,连接AD可知AD⊥BC,从而可求出△ABC的面积;根据圆周角定理,易求得∠EAF=2∠EPF=100°,圆的半径为2,可求出扇形AEF的面积;图中阴影部分的面积=△ABC的面积-扇形AEF的面积.
解答 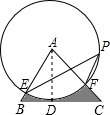 解:连接AD,
解:连接AD,
∵BC是切线,点D是切点,
∴AD⊥BC,
∴∠EAF=2∠EPF=100°,
∴S扇形AEF=$\frac{100π×{2}^{2}}{360}$=$\frac{10}{9}$π,
S△ABC=$\frac{1}{2}$AD•BC=$\frac{1}{2}$×2×6=6,
∴S阴影部分=S△ABC-S扇形AEF=6-$\frac{10}{9}$π.
故答案为:6-$\frac{10}{9}$π.
点评 本题考查了扇形面积的计算,同时用到了圆周角定理和切线的概念及性质等知识,解决本题的关键是利用圆周角与圆心角的关系求出扇形的圆心角的度数,难度一般.

练习册系列答案
相关题目
16.电视剧《宣言》展示了我县建立全国最早农村党支部的情形,某校为了了解学生对“广饶县最早农村党支部”的知晓情况,从全校2400名学生中随机抽取了100名学生进行调查,在这次调查中,样本是( )
| A. | 2400名学生 | |
| B. | 100名学生 | |
| C. | 所抽取的100名学生对“广饶县最早农村党支部”的知晓情况 | |
| D. | 每一名学生对“广饶县最早农村党支部”的知晓情况 |
14.甲、乙、丙三人站成一排拍照,则甲站在中间的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
1. 如图,直线AB∥CD,OG是∠EOB的平分线,∠EFD=70°,则∠BOG的度数是( )
如图,直线AB∥CD,OG是∠EOB的平分线,∠EFD=70°,则∠BOG的度数是( )
 如图,直线AB∥CD,OG是∠EOB的平分线,∠EFD=70°,则∠BOG的度数是( )
如图,直线AB∥CD,OG是∠EOB的平分线,∠EFD=70°,则∠BOG的度数是( )| A. | 70° | B. | 20° | C. | 35° | D. | 40° |
11.闽北某村原有林地120公顷,旱地60公顷,为适应产业结构调整,需把一部分旱地改造为林地,改造后,旱地面积占林地面积的20%,设把x公顷旱地改造为林地,则可列方程为( )
| A. | 60-x=20%(120+x) | B. | 60+x=20%×120 | C. | 180-x=20%(60+x) | D. | 60-x=20%×120 |