题目内容
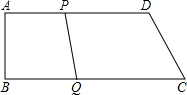 如图,在四边形ABCD中,AD∥BC,B=90°,AB=8cm,AD=25cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C出发,以3cm/s的速度向点B运动.规定其中一个运动到终点时,另一个也随之停止运动.从运动开始,使PQ∥CD和PQ=CD,分别需经过多少时间?为什么?
如图,在四边形ABCD中,AD∥BC,B=90°,AB=8cm,AD=25cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C出发,以3cm/s的速度向点B运动.规定其中一个运动到终点时,另一个也随之停止运动.从运动开始,使PQ∥CD和PQ=CD,分别需经过多少时间?为什么?考点:直角梯形,平行四边形的判定与性质,矩形的判定与性质,等腰梯形的性质
专题:动点型
分析:设点P、Q运动时间为t秒,得出AP=tcm,CQ=3tcm,PD=25-t,①当PQ∥CD时,得出方程25-t=3t,求出即可;当PQ与CD不平行,PQ=CD时,四边形PQCD为等腰梯形,分别过点P、D作PM⊥BC,DN⊥BC,垂足分别为M、N,则MN=PD=25-t,得出方程
(4t-25)=1,求出即可.
| 1 |
| 2 |
解答:解:设点P、Q运动时间为t秒,
则AP=tcm,CQ=3tcm,
∵AD=25cm,BC=26cm,
∴PD=AD-AP=25-t,
①当PQ∥CD时,又∵AD∥BC,即PD∥QC,
∴四边形PQCD为平行四边形,
∴PQ=CD,PD=CQ,
∴25-t=3t,
解得t=
s,即当t=
s时,PQ∥CD和PQ=CD;
②当PQ与CD不平行,PQ=CD时,四边形PQCD为等腰梯形.
如图2,分别过点P、D作PM⊥BC,DN⊥BC,
垂足分别为M、N,则MN=PD=25-t,
QM=CN=
(CQ-MN)=
(3t-25+t),
=
(4t-25),
∵在四边形ABCD中,AD∥BC,∠B=90°,
∴∠A=90°,
∵DN⊥BC,
∴∠BND=90°,
∴四边形ABND为矩形,
∴BN=AD=25,
∴QM=CN=BC-BN=26-25=1,
∴
(4t-25)=1,解得t=
<
.
综上,当t=
s时,PQ∥CD;当t=
s或t=
s时PQ=CD.
则AP=tcm,CQ=3tcm,
∵AD=25cm,BC=26cm,
∴PD=AD-AP=25-t,
①当PQ∥CD时,又∵AD∥BC,即PD∥QC,
∴四边形PQCD为平行四边形,
∴PQ=CD,PD=CQ,
∴25-t=3t,
解得t=
| 25 |
| 4 |
| 25 |
| 4 |

②当PQ与CD不平行,PQ=CD时,四边形PQCD为等腰梯形.
如图2,分别过点P、D作PM⊥BC,DN⊥BC,
垂足分别为M、N,则MN=PD=25-t,
QM=CN=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
∵在四边形ABCD中,AD∥BC,∠B=90°,
∴∠A=90°,
∵DN⊥BC,
∴∠BND=90°,
∴四边形ABND为矩形,
∴BN=AD=25,
∴QM=CN=BC-BN=26-25=1,
∴
| 1 |
| 2 |
| 27 |
| 4 |
| 26 |
| 3 |
综上,当t=
| 25 |
| 4 |
| 25 |
| 4 |
| 27 |
| 4 |
点评:本题考查了梯形的性质,矩形的性质和判定,平行四边形的性质的应用,题目是一道综合性比较强的题目,难度适中.

练习册系列答案
相关题目
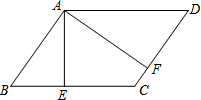 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F. 2013年我国中东部地区先后遭遇多次大范围雾霾天气,其影响范围、持续时间、雾霾强度历史少见,给人们生产生活造成了严重影响.为此“雾霾天气的主要成因”就成为某校环保小组调查研究的课题,他们随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
2013年我国中东部地区先后遭遇多次大范围雾霾天气,其影响范围、持续时间、雾霾强度历史少见,给人们生产生活造成了严重影响.为此“雾霾天气的主要成因”就成为某校环保小组调查研究的课题,他们随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=