题目内容
如图1,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m-420|+(2n-40)=0,射线OP从OB处绕点0以4度/秒的速度逆时针旋转.
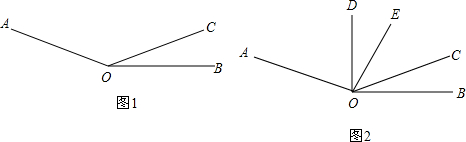
(1)试求∠AOB的度数;
(2)如图l,当射线OP从OB处绕点O开始逆时针旋转,同时射线OQ从OA处以l度/秒的速度绕点0顺时针旋转,当他们旋转多少秒时,使得∠POQ=10°?
(3)如图2,若射线OD为∠AOC的平分线,当射线OP从OB处绕点O开始逆时针旋转,同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转,使得这两条射线重合于射线OE处(OE在∠DOC的内部)时,且
=
,试求x.

(1)试求∠AOB的度数;
(2)如图l,当射线OP从OB处绕点O开始逆时针旋转,同时射线OQ从OA处以l度/秒的速度绕点0顺时针旋转,当他们旋转多少秒时,使得∠POQ=10°?
(3)如图2,若射线OD为∠AOC的平分线,当射线OP从OB处绕点O开始逆时针旋转,同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转,使得这两条射线重合于射线OE处(OE在∠DOC的内部)时,且
| ∠COE |
| ∠DOE+∠BOC |
| 4 |
| 5 |
考点:几何变换综合题,角的计算
专题:
分析:(1)先根据非负数的性质求得m=140,n=20,即得∠AOC=140°,∠BOC=20°,从而得到结果;(2)设他们旋转x秒时,使得∠POQ=10°,则∠AOQ=x°,∠BOP=4x°.分①当射线OP与射线OQ相遇前,②当射线OP与射线OQ相遇后,两种情况,结合旋转的性质分析即可;
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°,先根据角平分线的性质可得∠COD的度数,即可求得∠BOD的度数,再根据
=
即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,即可求得结果.
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°,先根据角平分线的性质可得∠COD的度数,即可求得∠BOD的度数,再根据
| ∠COE |
| ∠DOE+∠BOC |
| 4 |
| 5 |
解答: 解:(1)∵|3m-420|+(2n-40)2=0,
解:(1)∵|3m-420|+(2n-40)2=0,
∴3m-420=0且2n-40=0,
∴m=140,n=20,
∴∠AOC=140°,∠BOC=20°,
∴∠AOB=∠AOC-∠BOC=160°;
(2)设他们旋转x秒时,使得∠POQ=10°.则∠AOQ=x°,∠BOP=4x°.
①当射线OP与射线OQ相遇前有:∠AOQ+∠BOP+∠POQ=∠AOB=160°,
即:x+4x+10=160,
解得:x=30;
②当射线OP与射线OQ相遇后有:∠AOQ+∠BOP-∠POQ=∠AOB=160°,
即:x+4x-10=160,
解得:x=34.
答:当他们旋转30秒或34秒时,使得∠POQ=10°;
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°.
∵OD为∠AOC的平分线,
∴∠COD=
∠AOC=70°,
∴∠BOD=∠COD+∠BOC=70°+20°=90°.
∵
=
,
∴∠COE=
×90°=40°,∠DOE=30°,∠BOE=20°+40°=60°
即:4t=60,
∴t=15,
∴∠DOE=15x°,即:15x=30
解得 x=2.
 解:(1)∵|3m-420|+(2n-40)2=0,
解:(1)∵|3m-420|+(2n-40)2=0,∴3m-420=0且2n-40=0,
∴m=140,n=20,
∴∠AOC=140°,∠BOC=20°,
∴∠AOB=∠AOC-∠BOC=160°;
(2)设他们旋转x秒时,使得∠POQ=10°.则∠AOQ=x°,∠BOP=4x°.
①当射线OP与射线OQ相遇前有:∠AOQ+∠BOP+∠POQ=∠AOB=160°,
即:x+4x+10=160,
解得:x=30;
②当射线OP与射线OQ相遇后有:∠AOQ+∠BOP-∠POQ=∠AOB=160°,
即:x+4x-10=160,
解得:x=34.
答:当他们旋转30秒或34秒时,使得∠POQ=10°;
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°.
∵OD为∠AOC的平分线,
∴∠COD=
| 1 |
| 2 |
∴∠BOD=∠COD+∠BOC=70°+20°=90°.
∵
| ∠COE |
| ∠DOE+∠BOC |
| 4 |
| 5 |
∴∠COE=
| 4 |
| 9 |
即:4t=60,
∴t=15,
∴∠DOE=15x°,即:15x=30
解得 x=2.
点评:本题考查了旋转的性质,角的计算.应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 为增强学生体质,各校要求学生每天在校参加体育锻炼的时间不少于1小时.我区为了解初三学生参加体育锻炼的情况,对部分初三学生进行了抽样调查,并将调查统计图表绘制如下.请你根据图表中信息解答下列问题:
为增强学生体质,各校要求学生每天在校参加体育锻炼的时间不少于1小时.我区为了解初三学生参加体育锻炼的情况,对部分初三学生进行了抽样调查,并将调查统计图表绘制如下.请你根据图表中信息解答下列问题:
 如图,在矩形ABCD中,AB=4,AD=2,E、F分别是AB、CD上的点,且BE=DF,连接BF、DE.
如图,在矩形ABCD中,AB=4,AD=2,E、F分别是AB、CD上的点,且BE=DF,连接BF、DE.