题目内容
四边形ABCD∽四边形A1B1C1D1，它们的面积比为9：4，它们的对应对角线的比为 ，若它们的周长之差为16cm，则四边形ABCD的周长为 ．
考点：相似多边形的性质
专题：
分析：根据相似多边形面积比等于相似比的平方，对应对角线的比等于相似比可得它们的对应对角线的比为3：2；根据相似多边形面积比等于周长比的平方，四边形ABCD∽四边形A1B1C1D1，面积比9：4，则周长比3：2，周长差16cm，列出方程可得所求的周长．
解答：解：∵四边形ABCD∽四边形A1B1C1D1，它们的面积比为9：4，
∴它们的对应对角线的比为3：2，
周长比3：2，
设四边形周长分别为3x，2x，
所以3x-2x=16，
解得：x=16，
所以四边形ABCD的周长为3x=3×16=48cm．
故答案为3：2，48cm．
∴它们的对应对角线的比为3：2，
周长比3：2，
设四边形周长分别为3x，2x，
所以3x-2x=16，
解得：x=16，
所以四边形ABCD的周长为3x=3×16=48cm．
故答案为3：2，48cm．
点评：本题比较简单，主要考查了相似多边形的性质：相似多边形面积比等于相似比的平方，对应对角线的比等于相似比，对应周长的比等于相似比．
练习册系列答案
相关题目
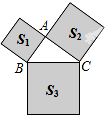如图，在△ABC中，∠BAC=90°，以△ABC的各边为边分别向外作正方形，S1、S2、S3分别表示这三个正方形的面积，S1=81，S3=225，则S2=
如图，D、E两点分别在△ABC的边BC、CA上，DE与AB不平行，当满足条件（写出一个即可）
把一张正方形纸条按如图那样折叠后，若得到∠AOB′=80°，则∠B′OG=
如图，在平行四边形ABCD中，E是AB的中点，CE和BD交于点O，若S△BOE=2，则S△DOC是（ ）| A、4 | B、6 | C、8 | D、9 |