题目内容
17．
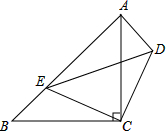如图，△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：△CDA≌△CEB．
分析 根据等腰直角三角形的性质得出CE=CD，BC=AC，再利用全等三角形的判定证明即可．
解答 证明：∵△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，
∴CE=CD，BC=AC，
∴∠ACB-∠ACE=∠DCE-∠ACE，
∴∠ECB=∠DCA，
在△CDA与△CEB中$\left\{\begin{array}{l}{BC=AC}\\{∠ECB=∠DCA}\\{EC=DC}\end{array}\right.$，
∴△CDA≌△CEB．
点评 本题考查了全等三角形的判定与性质，熟记等腰直角三角形的性质是解题的关键．
练习册系列答案
相关题目
5．已知xy＞0，化简二次根式$x\sqrt{-\frac{y}{x^2}}$的正确结果是（ ）
| A． | $-\sqrt{-y}$ | B． | $-\sqrt{y}$ | C． | $\sqrt{-y}$ | D． | $\sqrt{y}$ |
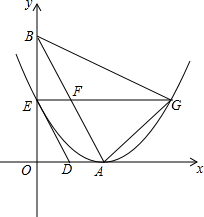如图，直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴，y轴分别交于点A，点B，两动点D，E分别从点A，点B同时出发向点O运动（运动到点O停止），运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒，设运动时间为t秒，以点A为顶点的抛物线经过点E，过点E作x轴的平行线，与抛物线的另一个交点为点G，与AB相交于点F．
如图，在△ABC中，AB=BC=4，S△ABC=4$\sqrt{3}$，点P、Q、K分别为线段AB、BC、AC上任意一点，则PK+QK的最小值为2$\sqrt{3}$．