题目内容
3.已知b=$\sqrt{a-3}$+$\sqrt{3-a}$+2a,解关于x的不等式组$\left\{\begin{array}{l}{ax-4<\frac{x}{2}+b}\\{\frac{x}{a}-\frac{x-7}{b}≥1}\end{array}\right.$.分析 首先根据二次根式有意义的条件求得a的值,则b即可求得,然后把a和b的值代入得到一个关于x的不等式组,解不等式组即可求解.
解答 解:根据题意得:a-3≥0且3-a≥0,
解得:a=3,
则b=2a=6.
则关于x的不等式是:$\left\{\begin{array}{l}{3x-4<\frac{x}{2}+6…①}\\{\frac{x}{3}-\frac{x-7}{6}≥1…②}\end{array}\right.$,
解①得:x<4,
解②得:x≥-1.
则不等式组的解集是:-1≤x<4.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
13.下列计算中,正确的是( )
| A. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B. | $\sqrt{8}+\sqrt{2}=\sqrt{10}$ | C. | $\sqrt{8}÷\sqrt{2}=4$ | D. | $\sqrt{8}×\sqrt{2}=4$ |
11.已知A,B,C三个数,其中A=-$\frac{\sqrt{2}}{2}$,B=0,C=-$\frac{1}{\sqrt{3}}$,则A,B,C的大小关系是( )
| A. | C>A>B | B. | B>A>C | C. | C>B>A | D. | B>C>A |
18.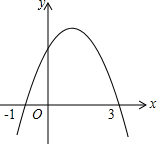 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
15.下列四个数中,最小的数是( )
| A. | -$\sqrt{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
 如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°40′,则∠B的度数为65°40′.
如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°40′,则∠B的度数为65°40′.