题目内容
6.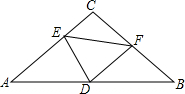 如图,在△ABC中,∠C=90°,AC=BC,点D为AB的中点,点E,F分别为AC,BC边上的动点,且CE=BF,当点E,F分别在边AC,BC上运动时,下列结论:
如图,在△ABC中,∠C=90°,AC=BC,点D为AB的中点,点E,F分别为AC,BC边上的动点,且CE=BF,当点E,F分别在边AC,BC上运动时,下列结论:①∠EDF=90°;
②△DEF为等腰直角三角形;
③S四边形CEDF=$\frac{1}{2}$S△ABC;
④EF=$\frac{1}{2}$AB.
其中正确的结论有①②③.(填序号)
分析 解答此题的关键是在于判断△DFE是否等腰直角三角形;作常规辅助线,连接CD,由SAS定理可得△ADE≌△CDF,从而可证∠EDF=90°可得DF=DE,可得△DFE是等腰直角三角形正确;再由补割法可证③是正确的.
解答 解:如图,连接CD,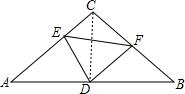
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
∵AC=BC,CE=BF,
∴AE=CF,
在△ADE和△CDF,
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCB}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF,
∴ED=DF,∠CDF=∠EDA,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
∴△DFE是等腰直角三角形,
故①②正确;
∵△ADE≌△CDF,
∴S△CDF=S△ADE,
∴S四边形CDFE=S△CDF+S△CDE=S△ADE+S△CDE=S△ADC=$\frac{1}{2}$S△ABC,故③正确;
∵点E,F分别在边AC,BC运动,
∴EF不一定等于$\frac{1}{2}$BC,
故④错误;
故答案为:①②③.
点评 此题考查的知识点有等腰直角三角形,全等三角形的判定与性质等知识点,综合性强,难度较大,是一道难题.利用“割补法”是求不规则图形的面积的常用方法.

练习册系列答案
相关题目
15.在下列描述数据的方法中,( )反映数据的频数分布.
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 直方图 |
 如图,每个小正方形的边长为1,三角形ABC的三个顶点都在格点(小正方形的顶点)上,
如图,每个小正方形的边长为1,三角形ABC的三个顶点都在格点(小正方形的顶点)上, 已知:正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,BF=2AF.画出∠EDF,猜想∠EDF的度数并写出计算过程.
已知:正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,BF=2AF.画出∠EDF,猜想∠EDF的度数并写出计算过程.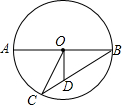 如图,半径为5的⊙O中,AB是直径,弦BC=8,OD⊥AB交BC于D,求CD的长及△OCD的面积.
如图,半径为5的⊙O中,AB是直径,弦BC=8,OD⊥AB交BC于D,求CD的长及△OCD的面积.
 如图,∵AC⊥AB,BD⊥AB(已知)
如图,∵AC⊥AB,BD⊥AB(已知)