题目内容
 如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面给出四个论断:
如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面给出四个论断:①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.
任选三个作为已知条件,余下一个作为结论,可得到几个命题?其中真命题有几个?分别给出证明.
考点:全等三角形的判定与性质,命题与定理
专题:
分析:任选三个作为已知条件,余下一个作为结论,可组合得到4个命题,分别为:
(1)①③④为条件,②为结论;
(2)①②④为条件,③为结论;
(3)①②③为条件,④为结论;
(4)②③④为条件,①为结论;
对4个命题分别证明即可解题.
(1)①③④为条件,②为结论;
(2)①②④为条件,③为结论;
(3)①②③为条件,④为结论;
(4)②③④为条件,①为结论;
对4个命题分别证明即可解题.
解答:解:(1)①③④为条件,②为结论;
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF;故本命题为真命题;
(2)①②④为条件,③为结论;
∵BE=CF,∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ABC=∠DEF;故本命题为真命题;
(3)①②③为条件,④为结论;
无法证明△ABC≌△DEF,故本命题不是真命题;
(4)②③④为条件,①为结论;
无法证明△ABC≌△DEF,故本命题不是真命题;
答:可得到4个命题,其中真命题有2个.
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS),
∴AC=DF;故本命题为真命题;
(2)①②④为条件,③为结论;
∵BE=CF,∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SSS),
∴∠ABC=∠DEF;故本命题为真命题;
(3)①②③为条件,④为结论;
无法证明△ABC≌△DEF,故本命题不是真命题;
(4)②③④为条件,①为结论;
无法证明△ABC≌△DEF,故本命题不是真命题;
答:可得到4个命题,其中真命题有2个.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABC≌△DEF是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为庆祝第十二届全运会的举办,中国邮政发行(第十二届全运会)邮票一套,价格为2.4元,另发行小全张,价格为3.6元,若茗茗买了m套邮票和n个小全张,则她共花费( )
| A、6mn元 |
| B、6(m+n)元 |
| C、(2.4n+3.6m)元 |
| D、(2.4m+3.6n)元 |
 如图,已知△ABC中,BE、CF分别是AC、AB边上的高,D是BC的中点,求证:DE=DF.
如图,已知△ABC中,BE、CF分别是AC、AB边上的高,D是BC的中点,求证:DE=DF.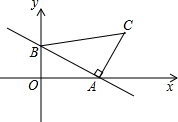 如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求过B,C两点的直线的表达式.
如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求过B,C两点的直线的表达式. 直线a∥b,b∥c,直线d与a相交于点A.
直线a∥b,b∥c,直线d与a相交于点A.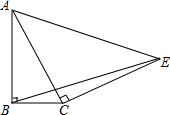 如图,在△ABC中,∠ABC=90°,过点C作AC的垂线CE,且CE=CA,连接AE、BE.
如图,在△ABC中,∠ABC=90°,过点C作AC的垂线CE,且CE=CA,连接AE、BE.