题目内容
9.AB是⊙O的非直径的弦,半径OA=2,∠AOB=120°,求弦AB的长.分析 根据题意画出图形,过点O作AB的垂线,得到直角三角形,在直角三角形中根据三角函数进行计算,然后再由垂径定理得到AB的长.
解答  解:如图:
解:如图:
过点O作OC⊥AB于C,则AC=BC,∠AOC=∠BOC=60°.
在直角△AOC中,sin60°=$\frac{AC}{AO}$,
∴AC=AOsin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴AB=2AC=2$\sqrt{3}$.
点评 本题考查的是解直角三角形,过圆心作弦的垂线,得到直角三角形,同时得到∠AOC=∠BOC=60°,在直角三角形中计算出AC的长,再根据垂径定理有AB=2AC,可以求出弦AB的长.

练习册系列答案
相关题目
4.下列式子中,是最简二次根式的有( )
①$\sqrt{{a}^{3}}$,②$\sqrt{m-2}$,③$\sqrt{\frac{x}{3}}$,④$\sqrt{8ab}$,⑤$\sqrt{{x}^{2}-{y}^{2}}$.
①$\sqrt{{a}^{3}}$,②$\sqrt{m-2}$,③$\sqrt{\frac{x}{3}}$,④$\sqrt{8ab}$,⑤$\sqrt{{x}^{2}-{y}^{2}}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.经过矩形的对称中心的任意一条直线把这个矩形分成两部分,设这两部分的面积分别为S1和S2,则S1和S2之间的关系是( )
| A. | S1>S1 | B. | S1<S2 | ||
| C. | S1=S2 | D. | S1和S2的大小关系无法确定 |
 如图所示,△ABC中,CD⊥AB于D,且AC>BC.
如图所示,△ABC中,CD⊥AB于D,且AC>BC.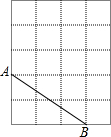 如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.
如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.
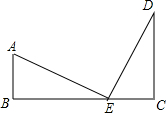 如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.
如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.