题目内容
3．半径为13cm的⊙O中，弦AB=10cm，则圆心O到AB的距离为12 cm．分析 过O作OE⊥AB于E，连接OA，根据垂径定理得出AE=BE=5cm，在Rt△AEO中，由勾股定理求出OE即可．
解答 解：如图，过O作OE⊥AB于E，连接OA，
根据垂径定理得：AE=BE，
∵AB=10cm，
∴AE=5cm，
在Rt△AEO中，由勾股定理得：OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12（cm），
即圆心O到AB的距离为12cm，
故答案为：12．
点评 本题考查了垂径定理，勾股定理的应用，解此题的关键是构造直角三角形，注意：垂直于弦的直径平分这条弦．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
13．对于解不等式$-\frac{2x}{3}＞\frac{3}{2}$，正确的结果是（ ）
| A． | $x＜-\frac{9}{4}$ | B． | $x＞-\frac{9}{4}$ | C． | x＞-1 | D． | x＜-1 |
如图，∠C=∠E，∠EAC=∠DAB，AB=AD．求证：BC=DE．
8．
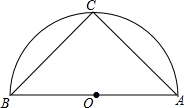如图，在以AB为直径的半圆O中，点C是$\widehat{AB}$的中点，若AC=4，则△ABC的面积是（ ）
如图，在以AB为直径的半圆O中，点C是$\widehat{AB}$的中点，若AC=4，则△ABC的面积是（ ）| A． | 3.5 | B． | 8 | C． | 12 | D． | 16 |
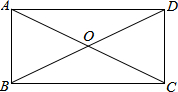如图，在四边形ABCD中，AC、BD交于点O，AO=CO，BO=DO，∠ABC=∠DCB．