题目内容
18. 如图,∠C=∠E,∠EAC=∠DAB,AB=AD.求证:BC=DE.
如图,∠C=∠E,∠EAC=∠DAB,AB=AD.求证:BC=DE.
分析 因为∠DAB=∠EAC,从图上可以看出∠DAB+∠BAE=∠EAC+∠BAE,即∠DAE=∠BAC,又因为,∠C=∠E,AB=AD,所以很容易证明△DAE≌△BAC,从而得出结论.
解答 证明:∵∠DAB=∠EAC,
∴∠DAB+∠BAE=∠EAC+∠BAE,
即∠DAE=∠BAC,
在△DAE和△BAC中$\left\{\begin{array}{l}{∠C=∠E}\\{∠BAC=∠DAE}\\{AB=AD}\end{array}\right.$,
∴△DAE≌△BAC,
∴BC=DE.
点评 本题考查全等三角形的判定定理,根据ASA可证明三角形全等,从而可得出结论.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.某餐饮公司为一所学校提供午餐,有10元、12元、15元三种价格的盒饭供师生选择,每人选一份,该校师生某一天购买的这三种价格盒饭数依次占50%、30%、20%,那么这一天该校师生购买盒饭费用的平均数和中位数分别是( )
| A. | 12元、12元 | B. | 12元、11元 | C. | 11.6元、12元 | D. | 11.6元、11元 |
6.下列命题中,真命题是( )
| A. | 有两边和一角对应相等的两个三角形全等 | |
| B. | 有两边和第三边上的高对应相等的两个三角形全等 | |
| C. | 有两边和其中一边上的高对应相等的两个三角形全等 | |
| D. | 有两边和第三边上的中线对应相等的两个三角形全等 |
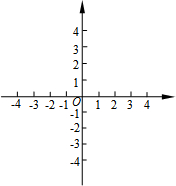 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0)、B(3,0).C(2,3)三点,且与y轴交于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0)、B(3,0).C(2,3)三点,且与y轴交于点D.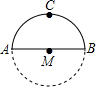 如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )
如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )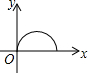



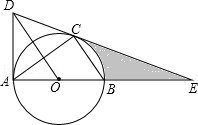 如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.