题目内容
12.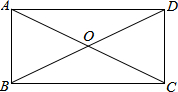 如图,在四边形ABCD中,AC、BD交于点O,AO=CO,BO=DO,∠ABC=∠DCB.
如图,在四边形ABCD中,AC、BD交于点O,AO=CO,BO=DO,∠ABC=∠DCB.(1)求证:四边形ABCD是矩形;
(2)要使四边形ABCD是正方形,请写出AC、BD还需要满足的条件.
分析 (1)利用平行四边形的判定方法得出四边形ABCD是平行四边形,进而得出∠ABC=90°,即可得出答案;
(2)利用正方形的判定得出矩形的对角线互相垂直进而得出答案.
解答 (1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴AB∥DC,
∴∠ABC+∠DCB=180°,
∵∠ABC=∠DCB,
∴∠ABC=90°,
∴四边形ABCD是矩形;
(2)要使四边形ABCD是正方形,AC、BD还需要满足的条件是:AC⊥BD.
点评 此题主要考查了矩形的判定以及正方形的判定,熟练应用矩形、正方形的判定是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列计算正确的是( )
| A. | (2a)2=2a2 | B. | a6÷a3=a3 | C. | a3-a2=a6 | D. | 3a2+2a3=5a3 |
4.已知△ABC的三个内角满足,∠B+∠C=2∠A,则∠A的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
1.顺次连接菱形ABCD各边中点所得到的四边形一定是( )
| A. | 菱形 | B. | 正方形 | ||
| C. | 矩形 | D. | 对角线互相垂直的四边形 |
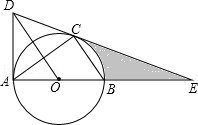 如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.