题目内容
17.函数y=$\sqrt{{x^2}+4x+5}+\sqrt{{x^2}-4x+8}$的最小值是5.分析 根据已知关系式得出抛物线的顶点坐标,再利用勾股定理以及对称点的性质得出最小值.
解答  解:∵x2+4x+5=(x+2)2+1,x2-4x+8=(x-2)2+4,
解:∵x2+4x+5=(x+2)2+1,x2-4x+8=(x-2)2+4,
∴即抛物线的顶点坐标分别为:(-2,1),(2,4),
即相当于求x轴上一点到(-2,1)和(2,2)的和的最小值,等价于(-2,-1)到(2,2)距离,
故如图所示:A′B=$\sqrt{{3}^{2}+{4}^{2}}$=5,即原式的最小值为5.
故答案为:5.
点评 此题主要考查了无理函数的最值问题,根据题意结合平面坐标系利用对称点求出是解题关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
12.设M=(4+2$\sqrt{3}$)3,其小数部分为P,则M(1-P)=( )
| A. | 58 | B. | 64 | C. | 73 | D. | 82 |
2.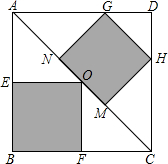 如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
 如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )| A. | $\frac{19}{36}$ | B. | $\frac{1}{2}$ | C. | $\frac{17}{36}$ | D. | $\frac{17}{32}$ |
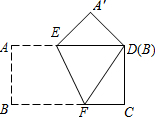 把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.
把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.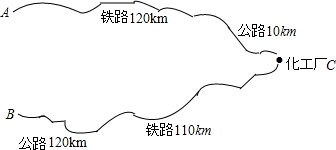 如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?
如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?