Question

8．如图，直线l的解析式为y=-$\frac{4}{3}$x+b，它与坐标轴分别交于A、B两点，其中B坐标为（0，4）．
（1）求出A点的坐标；
（2）若点 P在y轴上，且到直线l的距离为3，试求点P的坐标；（ 选做）
（3）在第一象限的角平分线上是否存在点Q使得∠QBA=90°？若存在，求点Q的坐标；若不存在，请说明理由．
（4）动点C从y轴上的点（0，10）出发，以每秒1cm的速度向负半轴运动，求出点C运动所有的时间t，使得△ABC为轴对称图形．

Answer 1

分析 （1）利用点B代入直线，求出直线解析式，然后求直线与x轴交点坐标；
（2）已知点到直线距离，可以做点到直线的垂线，构造直角三角形，利用三角形相似就出对应线段长度，继而求出点的坐标；
（3）点Q在第一象限角平分线上，设Q（x，x），已知给出了指定角，利用勾股定理列方程，即可求出点Q的坐标；
（4）由条件可知△ABC为等腰三角形，可设C点坐标为（0，y），则可用y分别表示出BC、AC，根据等腰三角形性质分AB=BC、AB=AC和BC=AC三种情况，可分别得到关于y的方程，可求得C点坐标，则可求得运动时间．

解答 解：
（1）将点B（0，4）代入直线l的解析式得b=4，
∴直线l的解析式为：y=-$\frac{4}{3}$x+4，
令y=0可得-$\frac{4}{3}$x+4=0，解得x=3，
∴A（3，0）；
（2）如图，过点P做直线AB的垂线，垂足为D，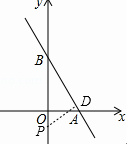

∵OB=4，OA=3，
∴AB=5，
∵∠B是公共角，∠BDP=∠BOD，
∴△BOA∽△BDP，
∴$\frac{OA}{PD}$=$\frac{AB}{BP}$，
∴$\frac{3}{3}$=$\frac{5}{BP}$，
∴BP=5，
∵OB=4，
∴当点P在B点上方进，PB=4+5=9，当点P在B点下方时，PB=4-5=-1，
∴P点坐标为（0，9）或（0，-1）；
（3）存在．理由如下：
∵Q在第一象限的角平分线上，
设Q（x，x），由勾股定理可得QB²+BD²=QD²，
∴x²+（x-4）²+5²=x²+（x-3）²，解得x=16，
∴Q（16，16），
即存在满足条件的Q点；
（4）设C点坐标为（0，y）（y≤10），则BC=|4-y|，AC=$\sqrt{{3}^{2}+{y}^{2}}$=$\sqrt{{y}^{2}+9}$，且AB=5，
当△ABC为轴对称图形，则△ABC为等腰三角形，
∴有AB=BC、AB=AC和BC=AC三种情况
①当AB=BC时，即|4-y|=5，解得y=9或y=-1，
∴C（0，9）或（0，-1），
∴t=10-9=1或t=10-（-1）=11，
即此时C点运动时间为1秒或11秒；
②当AB=AC时，即$\sqrt{{y}^{2}+9}$=5，解得y=4或y=-4，
∴C（0，4）或（0，-4），但当点C在x轴上方时不合题意，舍去，
∴t=10-（-4）=14，
即此时C点运动时间为14秒；
③当BC=AC时，即BC²=AC²，即|4-y|²=y²+9，解得y=$\frac{7}{8}$，
∴C（0，$\frac{7}{8}$），
∴t=10-$\frac{7}{8}$=$\frac{73}{8}$，
即此时C点运动时间为$\frac{73}{8}$秒；
综上可知当C点运动1秒、$\frac{73}{8}$秒、11秒或14秒时，使得△ABC为轴对称图形．

点评 本题为一次函数的综合应用，涉及点的坐标、相似三角形判定及性质、勾股定理、轴对称图形、等腰三角形的性质、分类讨论思想及方程思想等知识点．在（1）中利用B点坐标求得直线解析式即可求得A点坐标，在（2）中求得PB的长是解题的关键，在（3）中利用勾股定理得出关于Q点坐标的方程是解题的关键，在（3）中化动为静，求得C点的坐标是解题的关键．本题考查知识点较多，综合性较强，难度适中．