题目内容
3.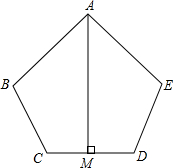 如图,在五边形ABCDE中,∠B=∠E,AB=AE,BC=ED,AM⊥CD,CM=3,求CD的长.
如图,在五边形ABCDE中,∠B=∠E,AB=AE,BC=ED,AM⊥CD,CM=3,求CD的长.
分析 连接AC和AD,根据SAS推出△ABC≌△AED,根据全等三角形的性质得出AC=AD,根据等腰三角形的性质得出即可.
解答 解:
连接AC和AD,
∵在△ABC和△AED中
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$
∴△ABC≌△AED,
∴AC=AD,
∵AM⊥CD,CM=3,
∴DM=CM=3,
∴CD=6.
点评 本题考查了全等三角形的性质和判定和等腰三角形的性质,能求出△ABC≌△AED是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列运算正确的是( )
| A. | 5a2+3a2=8a4 | B. | a3•a4=a12 | C. | (a+2b)2=a2+4b2 | D. | -$\root{3}{125}$=-5 |
8.在-$\sqrt{3}$,-1.5,-$\sqrt{2}$,-1这四个实数中,最小的实数是( )
| A. | -$\sqrt{3}$ | B. | -1.5 | C. | $-\sqrt{2}$ | D. | -1 |
13. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )| A. | 23° | B. | 22° | C. | 32° | D. | 33° |
 如图,AB=AC,BE与CF交于点O,且BO=CO,求证:∠B=∠C.
如图,AB=AC,BE与CF交于点O,且BO=CO,求证:∠B=∠C.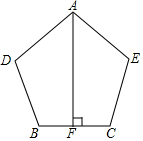 如图.AD=AE.BD=CE,AF⊥BC于点F,且F是BC的中点,求证:∠D=∠E.
如图.AD=AE.BD=CE,AF⊥BC于点F,且F是BC的中点,求证:∠D=∠E.