题目内容
17.若整式x2+ky2(k为不等于零的常数)能在有理数范围内因式分解,则k的值可以是-1(写出一个即可).分析 令k=-1,使其能利用平方差公式分解即可.
解答 解:令k=-1,整式为x2-y2=(x+y)(x-y),
故答案为:-1.
点评 此题考查了因式分解-运用公式法,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
12. 实数a,b在数轴上的对应点的位置如图所示,把-a,-b,0按照从小到大的顺序排列,正确的是( )
实数a,b在数轴上的对应点的位置如图所示,把-a,-b,0按照从小到大的顺序排列,正确的是( )
 实数a,b在数轴上的对应点的位置如图所示,把-a,-b,0按照从小到大的顺序排列,正确的是( )
实数a,b在数轴上的对应点的位置如图所示,把-a,-b,0按照从小到大的顺序排列,正确的是( )| A. | -a<0<-b | B. | 0<-a<-b | C. | -b<0<-a | D. | 0<-b<-a |
2.下列计算中,结果是a6的是( )
| A. | a2+a4 | B. | a2•a3 | C. | a12÷a2 | D. | (a2)3 |
1.若(x2+px-1)(x+1)的结果中不含x2项,则p的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
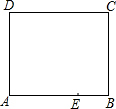 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5$\sqrt{2}$或4$\sqrt{5}$或5.
如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5$\sqrt{2}$或4$\sqrt{5}$或5.
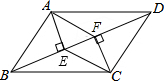 如图,在?ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.
如图,在?ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.