题目内容
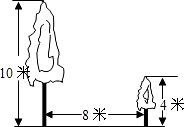 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行
如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行考点:勾股定理的应用
专题:
分析:根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
解答: 解:如图,设大树高为AB=10米,
解:如图,设大树高为AB=10米,
小树高为CD=4米,
过C点作CE⊥AB于E,则EBDC是矩形,
连接AC,
∴EB=4m,EC=8m,AE=AB-EB=10-4=6米,
在Rt△AEC中,AC=
=10米,
故答案为:10.
 解:如图,设大树高为AB=10米,
解:如图,设大树高为AB=10米,小树高为CD=4米,
过C点作CE⊥AB于E,则EBDC是矩形,
连接AC,
∴EB=4m,EC=8m,AE=AB-EB=10-4=6米,
在Rt△AEC中,AC=
| AE2+EC2 |
故答案为:10.
点评:本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
若cosα=
,则锐角α的大致范围是( )
| 2 |
| 3 |
| A、0°<α<30° |
| B、30°<α<45° |
| C、45°<α<60° |
| D、0°<α<30° |
 在△ABC中,M是AC的中点,P,Q为BC边的三等分点,BM与AP,AQ分别交于D,E两点,若△ABC的面积为40,则△ADE面积为
在△ABC中,M是AC的中点,P,Q为BC边的三等分点,BM与AP,AQ分别交于D,E两点,若△ABC的面积为40,则△ADE面积为 如图,已知E是?ABCD的边AB上一点,将△ADE沿直线DE折叠,点A恰好落在边BC上的点F处,如果△BEF的周长为7,△CDF的周长为15,那么CF的长等于
如图,已知E是?ABCD的边AB上一点,将△ADE沿直线DE折叠,点A恰好落在边BC上的点F处,如果△BEF的周长为7,△CDF的周长为15,那么CF的长等于 如图是一个轴对称图形,对称轴为直线l,图中点A、D关于直线l的对称点分别是点
如图是一个轴对称图形,对称轴为直线l,图中点A、D关于直线l的对称点分别是点 已知一次函数y=ax+b的图象如图,根据图中信息请写出不等式ax+b≥2的解集为
已知一次函数y=ax+b的图象如图,根据图中信息请写出不等式ax+b≥2的解集为 如图,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是
如图,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是