题目内容
如图，∠AOB是放置在正方形网格中的一个角，则sin∠AOB的值是考点：特殊角的三角函数值,勾股定理,勾股定理的逆定理
专题：网格型
分析：连接AB，利用勾股定理的逆定理证明△OAB是直角三角形，然后根据正弦函数的定义求解．
解答：
解：连接AB，
∵AB2=12+32=10，OB2=12+32=10，OA2=22+42=20，
∴AB2+OB2=OA2，
∴△OAB是直角三角形，
∴sin∠AOB=
=
=
．
故答案是：
．
解：连接AB，∵AB2=12+32=10，OB2=12+32=10，OA2=22+42=20，
∴AB2+OB2=OA2，
∴△OAB是直角三角形，
∴sin∠AOB=
| AB |
| OA |
| ||
|
| ||
| 2 |
故答案是：
| ||
| 2 |
点评：本题考查了三角函数的定义，正确证明△OAB是直角三角形是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
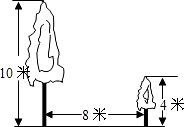如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行
已知如图，∠BOC和∠AOC的比是3：2，OD平分∠AOB，∠COD=10°，求∠AOB的度数．