题目内容
已知,在Rt△ABC中,∠C=90°,cosA、cosB是方程4x2-2(m+1)x+m=0的两个根,求m的值.
考点:根与系数的关系,根的判别式,互余两角三角函数的关系
专题:
分析:由cosA+cosB=
,cosAcosB=
,把cosA+cosB=
两边平方得2cosAcosB=(
)2-1,代入
求得m的数值即可,
| m+1 |
| 2 |
| m |
| 4 |
| m+1 |
| 2 |
| m+1 |
| 2 |
| m |
| 4 |
解答:解:∵cosA、cosB是方程4x2-2(m+1)x+m=0的两个根,
∴cosA+cosB=
,cosAcosB=
,
∴(cosA+cosB)2=(
)2,
∴2cosAcosB=(
)2-1,
即2×
=(
)2-1,
解得m=±
.
∴cosA+cosB=
| m+1 |
| 2 |
| m |
| 4 |
∴(cosA+cosB)2=(
| m+1 |
| 2 |
∴2cosAcosB=(
| m+1 |
| 2 |
即2×
| m |
| 4 |
| m+1 |
| 2 |
解得m=±
| 3 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图所示,在△ABC中,BD,CE分别是AC,AB边上的高,连接DE,试说明△ADE∽△ABC.
如图所示,在△ABC中,BD,CE分别是AC,AB边上的高,连接DE,试说明△ADE∽△ABC.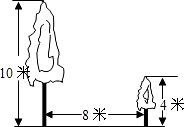 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行
如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行