题目内容
 如图,抛物线y=mx2+nx(m<0)和直线y=ax(a≠0),其中抛物线C′的顶点
如图,抛物线y=mx2+nx(m<0)和直线y=ax(a≠0),其中抛物线C′的顶点在直线y=ax上,且与x轴的一个交点为(6,0),则不等式的mx2+nx>ax解集是
考点:二次函数与不等式(组)
专题:
分析:由抛物线的图形可知c=0,即和x轴的一个交点坐标为(0,0),再由已知条件即可求出抛物线的对称轴,即抛物线C′的顶点横坐标,结合函数图象即可求出不等式的mx2+nx>ax解集.
解答:解:∵抛物线y=mx2+nx(m<0),
∴c=0,
∴图象和x轴的一个交点坐标为(0,0),
∵抛物线x轴的另一个交点为(6,0),
∴抛物线对称轴为直线x=
=3,
∴抛物线C′的顶点横坐标是3,
∴不等式的mx2+nx>ax解集是:0<x<3,
故答案为:0<x<3.
∴c=0,
∴图象和x轴的一个交点坐标为(0,0),
∵抛物线x轴的另一个交点为(6,0),
∴抛物线对称轴为直线x=
| 0+6 |
| 2 |
∴抛物线C′的顶点横坐标是3,
∴不等式的mx2+nx>ax解集是:0<x<3,
故答案为:0<x<3.
点评:本题考查二次函数与不等式,主要利用了联立两函数解析式求交点坐标的方法,利用函数图象求不等式的解集,利用数形结合的思想求解是更简便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )
如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )| A、落在菱形内 | B、落在圆内 |
| C、无法判断 | D、一样大 |
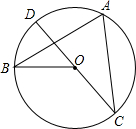 如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是
如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是 如图,已知AC和BD相交于点 O,∠AOB=∠A,∠COD=∠C.问∠A和∠C之间有什么大小关系?请说明理由.
如图,已知AC和BD相交于点 O,∠AOB=∠A,∠COD=∠C.问∠A和∠C之间有什么大小关系?请说明理由. 如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点
如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点