题目内容
15.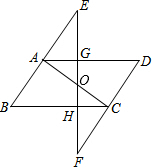 如图,在平行四边形ABCD中,E、F分别在BA、DC延长线上,且AE=CF,连接EF分别交AD、BC于G、H,求证:AC与GH互相平分.
如图,在平行四边形ABCD中,E、F分别在BA、DC延长线上,且AE=CF,连接EF分别交AD、BC于G、H,求证:AC与GH互相平分.
分析 先根据平行四边形的判定求出四边形AFCE是平行四边形,根据平行四边形的性质求出OE=OF,OA=OC,根据平行四边形的性质可得出∠E=∠F,∠EGA=∠FHC,利用AAS即可证明△EAG≌△FHC,继而可得出结论.
解答 证明:如图,连接AF和CE,
∵四边形ABCD是平行四边形,
∴AB∥CD,
即AE∥CF,
∵AE=CF,
∴四边形AFCE是平行四边形,
∴OE=OF,OA=OC,
∵E、F分别是平行四边形ABCD的边BA、DC延长线上的点,
∴BE∥DF,
∴∠E=∠F,
又∵平行四边形中AD∥BC,
∴∠EGA=∠EHB,
又∵∠EHB=∠FHC,
∴∠EGA=∠FHC,
在△EAG与△FHC中,
$\left\{\begin{array}{l}{∠E=∠F}\\{∠EGA=∠FHC}\\{AE=CF}\end{array}\right.$,
∴△EAG≌△FHC(AAS),
∴GE=FH,
∵OE=OF,
∴OG=OH,
∵OA=OC,
即AC与GH互相平分.
点评 本题考查了平行四边形的性质,解答本题的关键是掌握平行四边形的对边平行的性质及全等三角形的判定定理.

练习册系列答案
相关题目
19.若y=(a2+a)${x}^{{a}^{2}-2a-1}$是二次函数,那么( )
| A. | a=-1或a=3 | B. | a≠-1或a≠0 | C. | a=3 | D. | a=-1 |
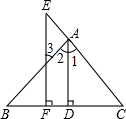 如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,试说明∠3=∠E.
如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,试说明∠3=∠E.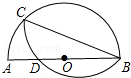 以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$.
以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$. 如图,添加条件:∠2=∠C,可以使AB∥DC,你的根据是同位角相等,两直线平行.
如图,添加条件:∠2=∠C,可以使AB∥DC,你的根据是同位角相等,两直线平行.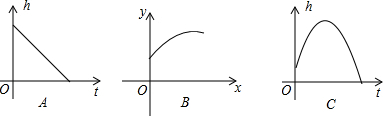
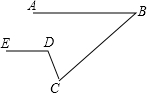 如图,已知AB∥DE,∠B=40°,∠EDC=110°,则∠C的度数为70°.
如图,已知AB∥DE,∠B=40°,∠EDC=110°,则∠C的度数为70°.