题目内容
已知直角△ABC中,∠C=90°,CA=5,CB=12,从C点向∠A、∠B的平分线作垂线,垂足分别为D、E,那么DE= .
考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:根据同角的余角相等求得∠DCN=∠DBC,进而求得∠DCN=∠DBF,∠CND=∠BFD,根据三角形内角和定理求得∠CND=∠BFD,得出∠BCD=∠BFD,从而求得BC=BF=12,CD=DF,同理证得AC=AG=5,CE=EG,根据三角形的中位线定理求得ED=
GF,依据勾股定理求得AB=13,根据BF+AG=AB+GF,BC+AC=AB+GF,求得GF=4,即可求得DE.
| 1 |
| 2 |
解答: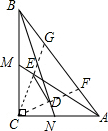 解:∵∠C=90°,CF⊥BD,
解:∵∠C=90°,CF⊥BD,
∴∠DCN=∠DBC,
∴∠BCD=∠BNC,
∵∠DBC=∠DBF,
∴∠DCN=∠DBF,
∵∠BDF=∠CDN=90°,
∴∠CND=∠BFD,
∴∠BCD=∠BFD,
∴BF=BC=12,
∴CD=DF,
同理可知AC=AG=5,CE=EG,
∴DE=
GF,
∵AB=
=
=13,BF+AG=AB+GF,
∴BC+AC=AB+GF,
即12+5=13+GF,
∴GF=4,
∴DE=2.
 解:∵∠C=90°,CF⊥BD,
解:∵∠C=90°,CF⊥BD,∴∠DCN=∠DBC,
∴∠BCD=∠BNC,
∵∠DBC=∠DBF,
∴∠DCN=∠DBF,
∵∠BDF=∠CDN=90°,
∴∠CND=∠BFD,
∴∠BCD=∠BFD,
∴BF=BC=12,
∴CD=DF,
同理可知AC=AG=5,CE=EG,
∴DE=
| 1 |
| 2 |
∵AB=
| AC2+BC2 |
| 52+122 |
∴BC+AC=AB+GF,
即12+5=13+GF,
∴GF=4,
∴DE=2.
点评:本题考查了勾股定理的应用,三角形的内角和定理,余角的性质,三角形的中位线定理,等腰三角形的性质等,求得GF的长是本题的关键.

练习册系列答案
相关题目
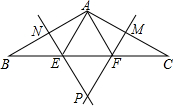 如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中:
如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中: