题目内容
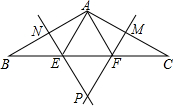 如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中:
如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中:①∠P=60°;
②∠EAF=60°;
③点P到点B和点C的距离相等;
④PE=PF.
正确的说法是
考点:线段垂直平分线的性质,角平分线的性质
专题:
分析:由分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F,可求得∠ANP=∠AMP=90°,又由△ABC中,∠BAC=120°,即可求得①∠P=60°;
易得AE=BE,AF=CF,即可求得∠BAE+∠CAF=∠B+∠C,继而求得②∠EAF=60°;
首先连接PA,PB,PC,即可得PA=PB=PC.
易得AE=BE,AF=CF,即可求得∠BAE+∠CAF=∠B+∠C,继而求得②∠EAF=60°;
首先连接PA,PB,PC,即可得PA=PB=PC.
解答:解:∵AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F,
∴∠ANP=∠AMP=90°,
∵△ABC中,∠BAC=120°,
∴∠P=360°-∠BAC-∠ANP-∠AMP=60°;故①正确;
∵AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F,
∴AE=BE,AF=CF,
∴∠BAE=∠B,∠CAF=∠C,
∵∠B+∠C=180°-∠BAC=60°,
∴∠BAE+∠CAF=60°,
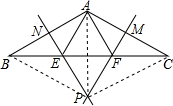 ∴∠EAF=∠BAC-(∠BAE+∠CAF)=60°,故②正确;
∴∠EAF=∠BAC-(∠BAE+∠CAF)=60°,故②正确;
连接PA,PB,PC,
∵AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F,
∴PA=PB,PA=PC,
∴PB=PC,
即点P到点B和点C的距离相等;故③正确;
∵△ABC不一定是等腰三角形,
∴BE不一定等于CF,
∴无法判定PE与PF是否相等,故④错误.
故答案为:①②③.
∴∠ANP=∠AMP=90°,
∵△ABC中,∠BAC=120°,
∴∠P=360°-∠BAC-∠ANP-∠AMP=60°;故①正确;
∵AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F,
∴AE=BE,AF=CF,
∴∠BAE=∠B,∠CAF=∠C,
∵∠B+∠C=180°-∠BAC=60°,
∴∠BAE+∠CAF=60°,
 ∴∠EAF=∠BAC-(∠BAE+∠CAF)=60°,故②正确;
∴∠EAF=∠BAC-(∠BAE+∠CAF)=60°,故②正确;连接PA,PB,PC,
∵AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F,
∴PA=PB,PA=PC,
∴PB=PC,
即点P到点B和点C的距离相等;故③正确;
∵△ABC不一定是等腰三角形,
∴BE不一定等于CF,
∴无法判定PE与PF是否相等,故④错误.
故答案为:①②③.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
(x2-px+3)(x-q)的乘积中不含x2项,则p、q的关系为( )
| A、相等 | B、互为倒数 |
| C、互为相反数 | D、无法确定 |