题目内容
一个正边形的每个外角都等于40°，则它的内角和是 °．
考点：多边形内角与外角
专题：
分析：由一个多边形的每个外角都等于40°，根据n边形的外角和为360°计算出多边形的边数n，然后根据n边形的内角和定理计算即可．
解答：解：设这个多边形是n边形，则
40°×n=360°，
解得n=9．
这个多边形的内角和为（9-2）×180°=1260°．
答：这个多边形的内角和为1260°．
故答案为：1260．
40°×n=360°，
解得n=9．
这个多边形的内角和为（9-2）×180°=1260°．
答：这个多边形的内角和为1260°．
故答案为：1260．
点评：本题考查了多边形的内角和外角，n边形的内角和定理：n边形的内角和=（n-2）•180°；注意熟记n边形的外角和为360°．
练习册系列答案
相关题目
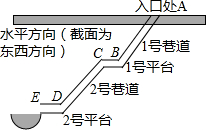如图是某煤矿地下巷道截面示意图，其中点A为入口，1号巷道与水平地面的夹角为30°，AB长为30米，1号平台BC长为5米，与水平地面平行，2号巷道与水平地面的夹角为45°，CD长为26米，2号平台ED长为8米，与水平地面平行．由于突发透水事故，在2号平台正西方出现险情，水位不断上涨，同时由于2号巷道正上方发生了塌方，阻断了救援人员的营救，被困于2号平台的6名工人面临着严峻的生死考验，事发后，抢险队果断作出决策，在入口A的正西方向某处向地下钻井抽水解救被困工人，根据你所学的知识，确定在距入口A处正西方多远处实施钻井施救较合理，并计算需要钻多深才能抽到水窖中的水？（结果精确到0.1米，参考数据：
如图，AB是⊙O直径，点D是弧AEB上的一个动点（不包括A，B），则下列结论：
如图，△ABC的三个顶点都在⊙O上，AD是直径，且∠CAD=50°，则∠B的度数为已知：2y=x+5，则代数式（x-2y）2-4y+2x的值为（ ）
| A、0 | B、15 | C、20 | D、-35 |
对于函数y=-2x+3，表述正确的是（ ）
| A、图象一定经过（-2，-1） |
| B、与坐标轴围成的三角形面积为4 |
| C、向右平移1个单位后的解析式是y=-2x+4 |
| D、x每增加1，y的值减小2 |