题目内容
3.若抛物线y=(x-m)2+2m-1(m是常数)与直线y=x+2有两个交点,且这两个交点分布在抛物线对称轴的同一侧,则m的取值范围3<m≤$\frac{13}{4}$.分析 根据二次函数y=(x-m)2+2m-1(m是常数)与直线y=x+2有两个交点,且这两个交点分别在抛物线对称轴的同侧,则(m-m)2+2m-1>m+2,结合根的判别式即可求出m的取值范围即可.
解答 解:∵抛物线y=(x-m)2+2m-1(m是常数)与直线y=x+2有两个交点,且这两个交点分别在抛物线对称轴的同一侧,
∴当x=m时,y<m+2,所以把x=m代入解析式中得:(m-m)2+2m-1>m+2,
∴m>3,
若y=(x-m)2+2m-1(m是常数)与直线y=x+2有两个交点,
则x2-2mx+m2+2m-1=x+2,
x2-(2m+1)x+m2+2m-3=0,
△=(2m+1)2-4(m2+2m-3)≥0,
即m≤$\frac{13}{4}$,
所以m的取值范围是3<m≤$\frac{13}{4}$.
故答案是:3<m≤$\frac{13}{4}$.
点评 本题考查了二次函数的性质的知识,解题的关键是得出当x=m时,y>m+2是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若(m+2)x=-1是关于x的一元一次方程,则m的取值是( )
| A. | m≠-2 | B. | m≠0 | C. | m≠2 | D. | m>2 |
11.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-3$\sqrt{2}$=1 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | $\sqrt{\frac{2}{3}}$×$\sqrt{6}$=2 |
18.抛物线y=(x+3)2-6的顶点坐标为( )
| A. | (3,-6) | B. | (-6,3) | C. | (-3,-6) | D. | (-6,-3) |
12. 如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )
如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )
 如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )
如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
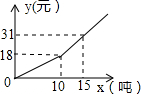 我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水18吨,则应交水费38.8元.
我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水18吨,则应交水费38.8元. 如图所示,矩形ABCD的两条对角线相交于点O,AD=8,AB=6,将△ABO向右平移得到△DCE,则△ABO向右平移过程扫过的面积是48.
如图所示,矩形ABCD的两条对角线相交于点O,AD=8,AB=6,将△ABO向右平移得到△DCE,则△ABO向右平移过程扫过的面积是48.