题目内容
18．已知实数x0，y0是方程组$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=|x|+1}\end{array}\right.$的解，求x0+y0的值．分析 当x0＜0时，由第二个方程可得到x0+y0的值；当x0＞0时，可求得$\frac{1}{{x}_{0}}$-x0，再利用完全平方公式可求得$\frac{1}{{x}_{0}}$+x0，即x0+y0的值．
解答 解：
∵x0，y0是方程组$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=|x|+1}\end{array}\right.$的解，
∴$\left\{\begin{array}{l}{{y}_{0}=\frac{1}{{x}_{0}}}\\{{y}_{0}=|{x}_{0}|+1}\end{array}\right.$，
当x0＜0时，则有y0=-x0+1，
∴x0+y0=1；
当x0＞0时，则有y0=x0+1，
∴$\frac{1}{{x}_{0}}$-x0=1，
∴（$\frac{1}{{x}_{0}}$+x0）2=（$\frac{1}{{x}_{0}}$-x0）2+2=3，
∵x0＞0，
∴$\frac{1}{{x}_{0}}$+x0＞0，
∴$\frac{1}{{x}_{0}}$+x0=$\sqrt{3}$，即x0+y0=$\sqrt{3}$，
综上可知x0+y0的值为1或$\sqrt{3}$．
点评 本题主要考查解方程组，利用分类思想把方程化为两种情况，再利用整体思想求解即可．注意完全平方公式的灵活运用．
练习册系列答案
相关题目
如图，在△ABC中，∠ACB=90°，CD为AB边上的中线，过点A作AE⊥CD于点E，过点B作CD平行线，交AE的延长线于点F，在延长线上截得FG=CD，连结CG、DF．若BG=11，AF=8，则四边形CGFD的面积等于20．
如图，分别以△ABC的边AB、AC为直角边向外作等腰Rt△ABD、Rt△ACE．连结BE、CD，且交于点Q，求证：OA平分∠DOE．
3．
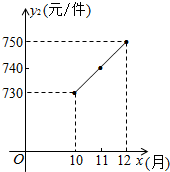某企业为重庆计算机产业基地提供电脑配件．受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y1（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：
随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格y2（元）与月份x（10≤x≤12，且x取整数）之间存在如图所示的变化趋势：
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1 与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
（2）若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤9，且x取整数），10至12月的销售量p2（万件）p2=-0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；
（3）今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少0.1a%．这样，在保证每月上万件配件销量的前提下，完成1至5月的总利润1700万元的任务，请你参考以下数据，估算出a的整数值．（参考数据：992=9801，982=9604，972=9409，962=9216，952=9025）
某企业为重庆计算机产业基地提供电脑配件．受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y1（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1（元/件） | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1 与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
（2）若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤9，且x取整数），10至12月的销售量p2（万件）p2=-0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；
（3）今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少0.1a%．这样，在保证每月上万件配件销量的前提下，完成1至5月的总利润1700万元的任务，请你参考以下数据，估算出a的整数值．（参考数据：992=9801，982=9604，972=9409，962=9216，952=9025）
10．下表是明明商行某商品的销售情况，该商品原价为560元，随着不同幅度的降价．
（1）每降价5元，日销量增加多少件？请你估计降价之前的日销量是多少？
（2）写出降价x（元）与日销量y（件）之间的关系式．
| 降价（单位：元） | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| 日销量（单位：件） | 780 | 810 | 840 | 870 | 900 | 930 | 960 |
（2）写出降价x（元）与日销量y（件）之间的关系式．
如图，?ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，∠ADC=54°，则∠AEB=36°．