题目内容
6.观察下列数,按规律填空.1,-$\frac{1}{3},\frac{1}{5},-\frac{1}{7}$,$\frac{1}{9}$,$-\frac{1}{11}$,$\frac{1}{13}$,第2015个数是$\frac{1}{2015}$.
分析 分母是从1开始的连续自奇数,分子都1,奇数位置为正,偶数位置为负,由此得出第n个数为(-1)n+1$\frac{1}{2n+1}$,进一步代入求得答案即可.
解答 解:这列数为1,-$\frac{1}{3},\frac{1}{5},-\frac{1}{7}$,$\frac{1}{9}$,-$\frac{1}{11}$,$\frac{1}{13}$,第2015个数是$\frac{1}{2015}$.
故答案为:$\frac{1}{9}$,-$\frac{1}{11}$,$\frac{1}{13}$,$\frac{1}{2015}$.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律,解决问题.

练习册系列答案
相关题目
14.圆的周长公式为C=2πr,下列说法正确的是( )
| A. | 常量是2 | B. | 变量是C、π、r | C. | 变量是C、r | D. | 常量是2、r |
 如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,则MN的长为2cm.
如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,则MN的长为2cm. 猜想并探究:
猜想并探究: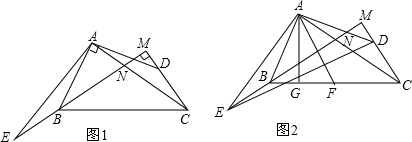
 如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是20.
如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是20.