题目内容
 六一儿童节前夕,儿童乐园准备将如图所示的滑梯重新油漆一遍.已知滑梯左侧是1米宽的滑道,右侧是1米宽的台阶,顶部是边长为1米的正方形平台(油漆部分为右侧台阶朝上和朝右的表面、顶部平台和滑梯上表面).现量得滑梯的高AC为2米,∠ABC=30°,∠EDC=45°,求需要油漆的总面积.
六一儿童节前夕,儿童乐园准备将如图所示的滑梯重新油漆一遍.已知滑梯左侧是1米宽的滑道,右侧是1米宽的台阶,顶部是边长为1米的正方形平台(油漆部分为右侧台阶朝上和朝右的表面、顶部平台和滑梯上表面).现量得滑梯的高AC为2米,∠ABC=30°,∠EDC=45°,求需要油漆的总面积.考点:解直角三角形的应用-坡度坡角问题
专题:压轴题
分析:在Rt△ABC中,根据三角函数可求AB的长,作EF⊥BD于F,根据梯形的性质和等腰直角三角形的性质可求FD=EF=2,再根据长方形的面积公式即可求解.
解答: 解:在Rt△ABC中,∵∠ABC=30°,
解:在Rt△ABC中,∵∠ABC=30°,
∴AB=AC÷sin30°=2÷
=4,
作EF⊥BD于F,则EF=AC=2,
∵∠EDC=45°,
∴FD=EF=2,
∴需要油漆的总面积为:(AB+AE+EF+FD-
)×1=(4+1+2+2-
)×1=
(m2).
 解:在Rt△ABC中,∵∠ABC=30°,
解:在Rt△ABC中,∵∠ABC=30°,∴AB=AC÷sin30°=2÷
| 1 |
| 2 |
作EF⊥BD于F,则EF=AC=2,
∵∠EDC=45°,
∴FD=EF=2,
∴需要油漆的总面积为:(AB+AE+EF+FD-
| 1 |
| 3 |
| 1 |
| 3 |
| 26 |
| 3 |
点评:考查了解直角三角形的应用-坡度坡角问题,本题需要油漆的总面积为:(AB+AE+EF+FD)×宽度.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
有6个数,0.245,0.3030030003,
,-π,tan60°,其中无理数的个数为( )
| 3 | 27 |
| A、1个 | B、2个 | C、3个 | D、4个 |
袋子里有黑球、红球和白球共1000个,为了了解各色球的个数,小刚经过实验了解到随机摸出一个是黑球的概率是
,是红球的概率是
,那么白球的个数是( )
| 7 |
| 20 |
| 13 |
| 50 |
| A、350 | B、260 |
| C、390 | D、510 |
 如图,在平面直角坐标系中,点A(2,3)为二次函数y=ax2+bx-2(a≠0)与反比例函数
如图,在平面直角坐标系中,点A(2,3)为二次函数y=ax2+bx-2(a≠0)与反比例函数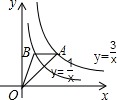 如图,点A和点B在第一象限,A是反比例函数y=
如图,点A和点B在第一象限,A是反比例函数y= 中小学生作业负担过重现象已经引起社会各界关注,各中小学校积极采取措施,“减负增效”势在必行.某中学在新学期开始就实行多种措施,力求“减负增效”,并取得理想效果.该校对在校300名学生就实施措施后的每日作业用时减水率进行随机调查,调查统计的数据制成如下统计图表:
中小学生作业负担过重现象已经引起社会各界关注,各中小学校积极采取措施,“减负增效”势在必行.某中学在新学期开始就实行多种措施,力求“减负增效”,并取得理想效果.该校对在校300名学生就实施措施后的每日作业用时减水率进行随机调查,调查统计的数据制成如下统计图表: