题目内容
 如图,在平面直角坐标系中,点A(2,3)为二次函数y=ax2+bx-2(a≠0)与反比例函数y=
如图,在平面直角坐标系中,点A(2,3)为二次函数y=ax2+bx-2(a≠0)与反比例函数y=| k |
| x |
| 1 |
| 2 |
(1)求二次函数和反比例函数的解析式;
(2)已知点M为抛物线上一点,且在第三象限,顺次连接点D、M、B、E,求四边形DMBE面积的最大值;
(3)在(2)中四边形DMBE面积最大的条件下,过点M作MH⊥x轴于点H,交EB的延长线于点F,Q为线段HF上一点,且点Q到直线BE的距离等于线段OQ的长,求Q点的坐标.
考点:二次函数综合题
专题:
分析:(1)把A(2,3)代入反比例函数的解析式即可求出k的值;由条件tan∠ADE=
可求出D的坐标,把A和D点的坐标代入到y=ax2+bx-2(a≠0)中求出a和b的值即可去吃二次函数的解析式;
(2)过M作MH⊥DE于H,设M的坐标为(a,
a2+
a-2),由题意可知S四边形DMBE=S△DHM+S四边形HOBM+S△OEB,进而得到S和a的二次函数关系,由函数的性质即可求出四边形DMBE面积的最大值;
(3)首先由抛物线的解析式可求出抛物线的对称轴,设过EB的直线为y=kx+b,由E和B的坐标即可求出其解析式,再通过△QPE∽△EHF,得到
=
,进而求出b的值,又Q在线段HF上,所以Q点的坐标可求出.
| 1 |
| 2 |
(2)过M作MH⊥DE于H,设M的坐标为(a,
| 1 |
| 2 |
| 3 |
| 2 |
(3)首先由抛物线的解析式可求出抛物线的对称轴,设过EB的直线为y=kx+b,由E和B的坐标即可求出其解析式,再通过△QPE∽△EHF,得到
| QP |
| EH |
| QF |
| EF |
解答:解:(1)将A(2,3)代入y=
中,
解得:k=6,
∴y=
,
又∵且tan∠ADE=
,
∴D(-4,0),
将A,D代入y=ax2+bx-2(a≠0)中得:
,
解得:
,
∴y=
x2+
x-2;
(2)过M作MH⊥DE于H,设M的坐标为(a,
a2+
a-2),
则S四边形DMBE=S△DHM+S四边形HOBM+S△OEB,
=
+
+
,
=
+1=2MH-a+1,
=2(-
a2-
a+2)-a+1,
=-a2-4a+5,
=-(a+2)2+9,
∴当a=-2时,四边形DMBE的面积最大为9;
(3)∵y=
x2+
x-2,
∴抛物线的对称轴为x=-
=-
,
∴点E的坐标为(1,0),
又∵B(0,-2),
∴EB的解析式为y=2x-2,
∴F的坐标为(-2,-6),
∴EF=
=3
,
设Q(-2,b),
∴FQ=b+6,QP=OQ=
,
∵△QPF∽△EHF,
∴
=
,
∴
=
,
∴20+5b2=(b+6)2,
∴b2-3b-4=0,
∴b1=4(舍),b2=-1,
又∵Q在线段HF上,
∴Q(-2,-1).
| k |
| x |
解得:k=6,
∴y=
| 6 |
| x |
又∵且tan∠ADE=
| 1 |
| 2 |
∴D(-4,0),
将A,D代入y=ax2+bx-2(a≠0)中得:
|
解得:
|
∴y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)过M作MH⊥DE于H,设M的坐标为(a,
| 1 |
| 2 |
| 3 |
| 2 |
则S四边形DMBE=S△DHM+S四边形HOBM+S△OEB,
=
| (a+4)•MH |
| 2 |
| (2+MH)•(-a) |
| 2 |
| 1×2 |
| 2 |
=
| aMH+4MH-2a-aMH |
| 2 |
=2(-
| 1 |
| 2 |
| 3 |
| 2 |
=-a2-4a+5,
=-(a+2)2+9,
∴当a=-2时,四边形DMBE的面积最大为9;
(3)∵y=
| 1 |
| 2 |
| 3 |
| 2 |
∴抛物线的对称轴为x=-
| b |
| 2a |
| 3 |
| 2 |
∴点E的坐标为(1,0),
又∵B(0,-2),
∴EB的解析式为y=2x-2,
∴F的坐标为(-2,-6),
∴EF=
| 32+62 |
| 5 |
设Q(-2,b),
∴FQ=b+6,QP=OQ=
| 4+b2 |
∵△QPF∽△EHF,
∴
| QP |
| EH |
| QF |
| EF |
∴
| ||
| 3 |
| b+6 | ||
3
|
∴20+5b2=(b+6)2,
∴b2-3b-4=0,
∴b1=4(舍),b2=-1,
又∵Q在线段HF上,
∴Q(-2,-1).
点评:此题考查了用待定系数法求二次函数、一次函数、反比例函数的解析式以及各种函数的性质和相似三角形的判定及其性质和一元二次方程的求解,题目的综合性很强,难度不小,对学生的解题能力要求很高.

练习册系列答案
相关题目
 如图,二次函数y=ax2+bx+c的图象与y轴负半轴相交,其顶点为(
如图,二次函数y=ax2+bx+c的图象与y轴负半轴相交,其顶点为(| 1 |
| 2 |
①ac<0;②a+b+c<0;③a-b+c<0;④a+b=0;⑤b2=4ac+4a.
其中正确的结论有( )
| A、5个 | B、4个 | C、3个 | D、2个 |
 如图,点B在∠CAD的平分线上,若添加一个适当的条件能使△ABC≌△ABD,所添加的条件不可以是( )
如图,点B在∠CAD的平分线上,若添加一个适当的条件能使△ABC≌△ABD,所添加的条件不可以是( )| A、∠C=∠D |
| B、AC=AD |
| C、∠CBE=∠DBE |
| D、BC=BD |
 六一儿童节前夕,儿童乐园准备将如图所示的滑梯重新油漆一遍.已知滑梯左侧是1米宽的滑道,右侧是1米宽的台阶,顶部是边长为1米的正方形平台(油漆部分为右侧台阶朝上和朝右的表面、顶部平台和滑梯上表面).现量得滑梯的高AC为2米,∠ABC=30°,∠EDC=45°,求需要油漆的总面积.
六一儿童节前夕,儿童乐园准备将如图所示的滑梯重新油漆一遍.已知滑梯左侧是1米宽的滑道,右侧是1米宽的台阶,顶部是边长为1米的正方形平台(油漆部分为右侧台阶朝上和朝右的表面、顶部平台和滑梯上表面).现量得滑梯的高AC为2米,∠ABC=30°,∠EDC=45°,求需要油漆的总面积.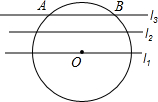 如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为3.点O在直线l1上,⊙O与直线的交点为A、B.且AB=8,则⊙O的半径
如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为3.点O在直线l1上,⊙O与直线的交点为A、B.且AB=8,则⊙O的半径