题目内容
在一个不透明的袋子中有4个标号分别为1,2,3,4的完全相同的小球,摸出一个球后不放回,再摸出一个球,两次摸到的球标号都是偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸到的球标号都是偶数的情况,再利用概率公式求解即可求得答案.注意此题属于不放回实验.
解答:解:画树状图得:

∵共有12种等可能的结果,两次摸到的球标号都是偶数的有2种情况,
∴两次摸到的球标号都是偶数的概率是:
=
.
故选A.

∵共有12种等可能的结果,两次摸到的球标号都是偶数的有2种情况,
∴两次摸到的球标号都是偶数的概率是:
| 2 |
| 12 |
| 1 |
| 6 |
故选A.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
已知二次函数y=2(x-3)2+
,它的顶点坐标为( )
| 3 |
| 2 |
A、(3,
| ||||
B、(-3,
| ||||
C、(
| ||||
D、(
|
因式分解-2a2+8ab-8b2结果正确的是( )
| A、-2(a2-4ab+4b2) |
| B、-2(a-2b)2 |
| C、-2(a+2b)2 |
| D、2(a-2b)2 |
 如图,点B在∠CAD的平分线上,若添加一个适当的条件能使△ABC≌△ABD,所添加的条件不可以是( )
如图,点B在∠CAD的平分线上,若添加一个适当的条件能使△ABC≌△ABD,所添加的条件不可以是( )| A、∠C=∠D |
| B、AC=AD |
| C、∠CBE=∠DBE |
| D、BC=BD |
下面图形中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 六一儿童节前夕,儿童乐园准备将如图所示的滑梯重新油漆一遍.已知滑梯左侧是1米宽的滑道,右侧是1米宽的台阶,顶部是边长为1米的正方形平台(油漆部分为右侧台阶朝上和朝右的表面、顶部平台和滑梯上表面).现量得滑梯的高AC为2米,∠ABC=30°,∠EDC=45°,求需要油漆的总面积.
六一儿童节前夕,儿童乐园准备将如图所示的滑梯重新油漆一遍.已知滑梯左侧是1米宽的滑道,右侧是1米宽的台阶,顶部是边长为1米的正方形平台(油漆部分为右侧台阶朝上和朝右的表面、顶部平台和滑梯上表面).现量得滑梯的高AC为2米,∠ABC=30°,∠EDC=45°,求需要油漆的总面积.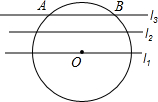 如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为3.点O在直线l1上,⊙O与直线的交点为A、B.且AB=8,则⊙O的半径
如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为3.点O在直线l1上,⊙O与直线的交点为A、B.且AB=8,则⊙O的半径 如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论: