题目内容
函数y=(3x+6)2的图象是由函数 的图象向左平移5个单位得到的,其图象开口向 ,对称轴 ,顶点坐标是 ,当x 时,y随x的增大而增大,当x= 时,y有最 值是 .
考点:二次函数图象与几何变换
专题:
分析:先将y=(3x+6)2变形为y=9(x+2)2,再根据“左加右减”的平移规律可得出函数y=(3x+6)2的图象是由函数y=9(x-3)2的图象向左平移5个单位长度得到的;然后根据函数解析式写出对称轴,顶点坐标,并根据二次函数的增减性和最值问题解答.
解答:解:∵y=(3x+6)2=9(x+2)2,
∴函数y=(3x+6)2的图象是由函数y=9(x-3)2的图象向左平移5个单位长度得到的,
其图象开口向上,对称轴是直线x=-2,顶点坐标是(-2,0);
当x>-2时,y随x的增大而增大;
当x=-2时,y有最小值是0.
故答案为:y=9(x-3)2,上,直线x=-2,(-2,0),>-2,-2,小,0.
∴函数y=(3x+6)2的图象是由函数y=9(x-3)2的图象向左平移5个单位长度得到的,
其图象开口向上,对称轴是直线x=-2,顶点坐标是(-2,0);
当x>-2时,y随x的增大而增大;
当x=-2时,y有最小值是0.
故答案为:y=9(x-3)2,上,直线x=-2,(-2,0),>-2,-2,小,0.
点评:本题考查了二次函数图象与几何变换,二次函数的顶点坐标,增减性,最值问题,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
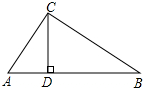 如图,△ABC中,∠ACB=90°,CD是高,若AB=13cm,AC=5cm,求CD的长.
如图,△ABC中,∠ACB=90°,CD是高,若AB=13cm,AC=5cm,求CD的长. 已知BD为∠ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F.求证:点E、F关于BD对称.
已知BD为∠ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F.求证:点E、F关于BD对称.