题目内容
如图，在面积为48的直角△ABC中，∠ACB=90°，CD⊥于AB于点D，点M、F、E分别在线段CD、CA、AD上，点N、G、H分别在线段DC、CB、BD上（M、N重合），且四边形DMFE，DNGH都为矩形，求两矩形面积和的最大值．考点：相似三角形的判定与性质,二次函数的最值
专题：常规题型
分析：根据平行可证
+
=1，设
=x，可以求得两矩形面积和的函数式，即可求得最大值．
| FG |
| AB |
| EF |
| CD |
| FG |
| AB |
解答：解：∵四边形DMFE，DNGH都为矩形，
∴
=
，
=
，
∵CF+AF=AC，
∴
+
=1，
设
=x，则
=1-x，
∵△ABC面积为48，
∴AB•CD=96．
∴两矩形面积和=EF•FG=AB•x•CD•（1-x）=96x（1-x）=-96(x-
)2+24．
∴
| FG |
| AB |
| CF |
| AC |
| AF |
| AC |
| EF |
| CD |
∵CF+AF=AC，
∴
| FG |
| AB |
| EF |
| CD |
设
| FG |
| AB |
| EF |
| CD |
∵△ABC面积为48，
∴AB•CD=96．
∴两矩形面积和=EF•FG=AB•x•CD•（1-x）=96x（1-x）=-96(x-
| 1 |
| 2 |
点评：本题考查了相似三角形对应边比例相等的性质，考查了函数式求最值问题．
练习册系列答案
阶梯计算系列答案
相关题目
在下面各数中无理数的个数有（ ）
|-
|，-3.14，
，0.1010010001…，+1.99，-
．
|-
| 3 |
| 4 |
| 22 |
| 7 |
| π |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
如图，已知△ABC中，AD，BF为BC，AC边上的高，过D作AB的垂线交AB于E，交BF于G，交AC的延长线于H，求证：DE2=EG•EH．
如图，在四边形ABCD中，∠ACB=∠BAD=105°，∠ABC=∠ADC=45°，求证：CD=AB．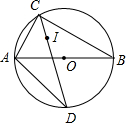
如图，AB是⊙O的直径，点C是⊙O上一点，点I是△ABC（AC＜AB）的内心，CI的延长线交⊙O于点D，连AD．
如图，在△ABC中，AB=8，AC=6，BC=10．线段BC所在直线以每秒2个单位的速度沿与其垂直的方向上平行移动，记x秒时，该直线在△ABC内的部分的长度为y．试写出y关于x的函数关系式，并在平面直角坐标系中画出这一函数的图象．如果一个正多边形绕它的中心旋转90°就和原来的图形重合，那么这个正多边形是（ ）
| A、正三角形 | B、正方形 |
| C、正五边形 | D、正六边形 |