题目内容
12.一元二次方程mx2-2x+1=0总有实数根,则m应满足的条件是( )| A. | m>1 | B. | m≤1 | C. | m<1 | D. | m≤1且m≠0 |
分析 根据一元二次方程的定义和判别式的意义得到m≠0且△=(-2)2-4m≥0,然后求出m的取值范围即可.
解答 解:∵一元二次方程mx2-2x+1=0总有实数根,
∴△≥0,m≠0,
∴(-2)2-4m≥0,
∴m≤1,
∴m≤1且m≠0.
故选D.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
2.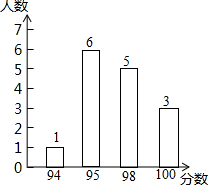 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )| A. | 98,95 | B. | 98,98 | C. | 95,98 | D. | 95,95 |
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 正五边形 | D. | 等腰三角形 |
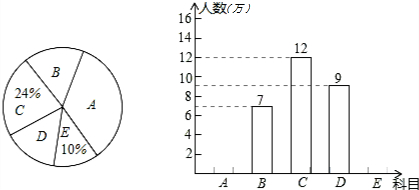 园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).
园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).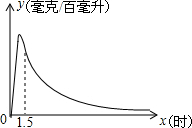 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示). 如图,∠B=∠C,AB=AC,△ABE与△ACD全等吗?为什么?
如图,∠B=∠C,AB=AC,△ABE与△ACD全等吗?为什么? 已知,如图,直线l和直线m分别是线段AB和线段AC的垂直平分线,O为交点,求证:点O到点A,B,C的距离相等.
已知,如图,直线l和直线m分别是线段AB和线段AC的垂直平分线,O为交点,求证:点O到点A,B,C的距离相等.