题目内容
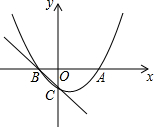
14.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 由y=mx(m≠0),y随x的增大而减小,推出m<0,可知二次函数y=mx2+m的图象的开口向下,与y则交于负半轴上,由此即可判断.
解答 解:∵y=mx(m≠0),y随x的增大而减小,
∴m<0,
∴二次函数y=mx2+m的图象的开口向下,与y则交于负半轴上,
故选A.
点评 本题参考二次函数的性质、正比例函数的性质等知识,解题的关键是熟练掌握正比例函数以及二次函数的性质,属于中考常考题型.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2017次后形成的图形中所有正方形的面积和是( )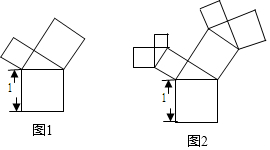

| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
2.如果点P1(x1,y1),P2(x2,y2),P3(x3,y3)在某双曲线上,且x1<x2<0<x3,则y1,y2,y3的大小关系可能为( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2<y3<y1 | D. | y3>y2>y1 |
9. 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )
 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )| A. | 2.5 | B. | 2.4 | C. | $\sqrt{6}$ | D. | $\sqrt{5}$ |
15.下列式子中,正确运用分数的基本性质的是( )
| A. | $\frac{1}{2}$=$\frac{1+2}{2+4}$=$\frac{3}{6}$ | B. | $\frac{2}{3}$=$\frac{2×2}{3×3}$=$\frac{4}{9}$ | C. | $\frac{7}{5}$=$\frac{7×0}{5×0}$=0 | D. | $\frac{3}{5}$=$\frac{3×4}{5×4}$=$\frac{12}{20}$ |
 如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为360°.
如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为360°.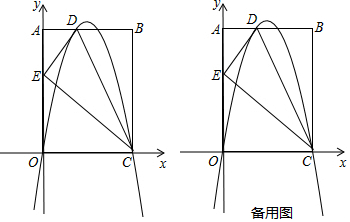
 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于C,与x轴帕交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于C,与x轴帕交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).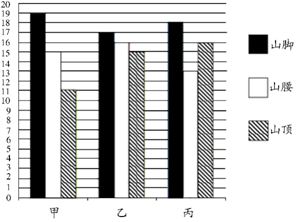 甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断: